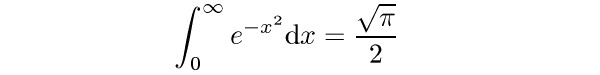
Portál AbcLinuxu, 29. ledna 2026 09:36
Matematici po staletí využívají plochu papíru k zaznamenání svých abstraktních myšlenek daleko kreativněji, než poskytuje běžná textová sazba: používají větší množství abeced, velikostí, značné množství speciálních značek. Vzájemné umístění znaků na papíře není vždy jen na jediném řádku. Sazárny účtovaly matematickou sazbu podle centimetru čtverečního (na rozdíl od počtu znaků v textu) a tato sazba byla drahá. Na památku toho ji ve zdrojovém textu TeXu vyznačujeme pomocí dolarů.
Knuth si dal velmi záležet na tom, aby TeX zvládal matematickou sazbu co nejlépe. Ukážeme si, s čím se potýkal a jak to vyřešil.
K zápisu matematického vzorečku v TeXu stačí znát názvy použitých značek
a výraz zhruba zapsat tak, jak bychom ho anglicky přečetli. Závorky
{} nebudou v sazbě vidět a vyznačují úseky, které jsou samy
„lokálním“ vzorečkem. Pomocí znaků ^ a _ se vyznačují
exponenty a indexy. Celý vzorec je třeba obklopit do dolarů : $...$
nebo dvojdolarů $$...$$. V prvém případě budeme mít vzoreček uvnitř
odstavce, ve druhém na samostatném řádku. Například
$$ \int_0^\infty e^{-x^2} {\rm d}x = {\sqrt\pi \over 2} $$
dá tento výsledek:
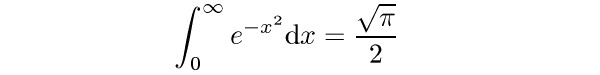
Matematici si na TeXový zápis poměrně rychle zvykli. Často píšou svoje myšlenky přímo do počítače v TeXu bez potřeby vidět, jak vzoreček dopadne, a vyměňují si v této notaci své názory například v emailech.
Za pozornost v předchozí ukázce stojí zápis zlomku ve tvaru
{čitatel \over jmenovatel}, ve kterém závorky {} vyznačují
hranici zlomku a \over odpovídá myšlence „napsat vzorec tak, jak
bychom ho anglicky přečetli“. Často se místo tohoto klasického TeXového zápisu
zlomku setkáváme spíš s užitím makra \frac{čitatel}{jmenovatel}, což
působí více programátorsky a strukturovaněji. Makro \frac je
definováno jednoduše:
\def\frac#1#2{{#1\over#2}}
Nejčastěji se ve vzorci vyskytuje proměnná nebo písmenem označený libovolný
matematický objekt (množina, funkce, prvek, vrchol). Takové písmeno musí být
v kurzívě, zatímco ostatní znaky (operátory, relace, číslice, závorky)
musejí být v antikvě. O to se stará TeX sám, takže stačí napsat
$$a+b=c$$ a máme proměnné v kurzívě a znaky plus, rovná se
v antikvě. Tedy:
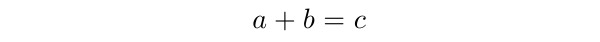
Někdy se ve vzorečku setkáme místo kurzívy s antikvou i pro písmena. Například při sazbě zkratek funkcí, operací nebo při psaní fyzikálních jednotek.
$$\sin^2 x + \cos^2 x = 1,\quad a = b \pmod c,\quad E = mc^2\ [{\rm J}]$$
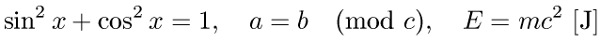
Pro kurzívu v matematických vzorcích Knuth vytvořil v písmu Computer
Modern speciální font (1) cmmi, který se liší od textové kurzívy (2)
cmti tím, že je mírně širší a v matematických vzorcích
čitelnější. Neškolené oko ale moc nepozná rozdíl.
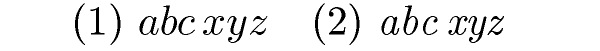
Ačkoli je ta kurzíva odlišná, je vytvořena ze stejných zdrojů jen vhodně odlišnou parametrizací v Metafontu. Je-li použita jiná rodina písma než Computer Modern, není obvykle speciální kurzíva přístupná, takže je třeba i v matematických vzorcích použít běžnou textovou kurzívu tohoto písma.
Deklarace písma pro matematiku se provádí v souboru maker a je
pro laika poměrně komplikovaná, protože nabízí poměrně velké možnosti.
PlainTeX implicitně zavádí písmo z rodiny Computer Modern. CSplain nabízí
soubory maker ams-tex.tex pro rozšířenou sadu Computer Modern
a tx-math.tex pro zavedení TX fontů. LaTeX má na zavedení
matematických fontů desítky různých makrobalíčků.
Jen málo matematických operátorů či dalších znaků najdeme přímo na klávesnici (plus, mínus, rovná se). Vesměs všechny další se zapisují pomocí vyhrazených názvů.
\pm, \times, \circ, \cap, \cup, \oplus, \leq, \geq, \sim, \in, \subset, \cdots, \ldots
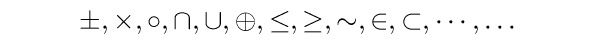
Toto je jen příklad. Ve skutečnosti jsou k dispozici stovky znaků, bez nichž se složitější sazba neobejde. V uživatelských příručkách k TeXu najdeme tabulky těchto znaků.
Všechny matematické znaky v TeXu jsou deklarovány na úrovni makrojazyka
pomocí „mathkódů“. Ty vyznačují, ze kterého fontu a slotu je třeba znak
vyzvednout, a dále, jakého typu znak je: obyčejný objekt, binární operátor,
relace, otevírací/zavírací závorka atd. Podle typu znaku TeX pozná, jaké má vložit
mezi znaky mezery. Například ve vzorci $1+1=2$ TeX pozná, že čísla jsou
obyčejné objekty, plus je binární operátor a rovnítko je relace. Na základě
toho vloží kolem binárního operátoru mírné mezery a kolem relace mírně větší
mezery (1). Uživatel toto mezerování neřeší, výsledek dopadne stejně, když napíše
$1+1=2$ i $1 + 1 = 2$, protože vstupní mezery mezi dolary
TeX ignoruje. Na druhé straně, bez použití dolarů (v textovém módu) dopadne ten
vzoreček v obou případech mizerně: buď tam nemáte žádné mezery (2), nebo tam
jsou velké mezery (3).
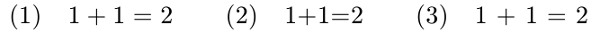
Některé operátory (suma, integrál) se nazývají „velké operátory“. Ve vzorci uvnitř odstavce jsou menší a na samostatném řádku větší. Indexy a exponenty v tomto případě fungují jako popisky k operátorům, které se v sazbě umisťují typicky nad a pod operátor:
$$ \sum_{k=0}^\infty {1\over 2^k} = 2 $$
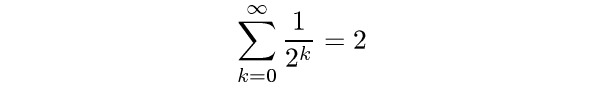
Povšimněte si, že je rozdíl, když napíšete znak mínus mezi dolary:
$-1$ a bez dolarů: -1. V prvém případě (1)
dostanete správně mínus, ve druhém (2) nesprávně spojovník, který svědčí
o tom, že to vysázel nějaký diletant, který nerozpozná spojovník od mínusu.
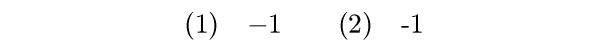
Při označování všeho možného matematikům záhy dojdou písmena latinské abecedy.
V takovém případě použijí alternativní abecedy, mezi kterými je nejčastěji
využita abeceda řecká (1) $\alpha\beta\gamma$, pak kaligrafické
znaky (2) $\cal ABC$ nebo (3) $\script ABC$,
dále fraktura (4) $\frak ABC$ a zdvojené
znaky (5) $\bbchar ABC$.
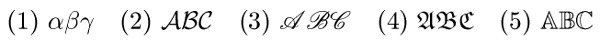
Při návrhu matematického fontu tedy nestačí připravit stovky až tisíce různých značek, ale též tyto další matematické abecedy. Vše musí mít pro zvolenou rodinu textového písma jednotný ráz. Dlouhou dobu neexistovala jiná úplná výbava písma pro matematiku než Computer Modern, protože udělat pořádný matematický font není žádná legrace. TeX sice řeší nastavení fontu pro textovou sazbu a pro matematiku zcela nezávisle, ale vyměnit jen sazbu textů za jiné písmo a ponechat matematiku v Computer Modern skoro jistě povede k paskvilu. Je to tím, že většina písem je odvozena z dynamické nebo přechodové antikvy, zatímco Computer Modern je statická antikva, která se k dynamické vůbec nehodí.
Později vznikly varianty matematického písma Euler, Lucida a Times. Dnes je k dispozici několik dalších matematických rodin písma: TXfonts (pro Times), TeXgyre math fonts (Pagella, Termes, Bonum), XITS (pro Times), Asana, Cambria math, Minion.
Pro indexy resp. exponenty se používá sazba typicky zmenšená na 70 % a pro indexy indexů resp. exponenty exponentů (a další možné kombinace) je vhodné písmo zmenšit na 50 % základní velikosti. Další zmenšování už se neužívá, tj. indexy indexů indexů už mají stejnou velikost jako indexy indexů.
Pomocí maker TeXu se pro indexy a indexy indexů (resp exponenty) zavádějí
fonty zcela zvlášť a mohou mít velikost nastavenu libovolně. Navíc
to mohou být fonty, které nezmenšují svou velikost jen tupě geometricky,
ale jsou pro menší sazbu speciálně uzpůsobeny (zejména s ohledem na
lepší čitelnost v malých velikostech). Například pro základní
sazbu matematické kurzívy v 10pt je v plainTeXu zaveden
font (1) cmmi10, pro indexy (2) cmmi7
a pro indexy indexů (3) cmmi5. Jsou to různé fonty, což
poznáme, když je všechny geometricky zvětšíme na společnou velikost (4).
V Metafontu jsou všechny tyto fonty vykresleny společným programem jen
s odlišnou parametrizací.
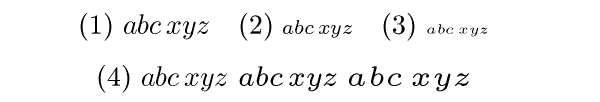
Podobně Knuth připravil rozdílně vykreslené fonty pro různé velikosti vesměs všech řezů písma Computer Modern (antikva, textová kurzíva, tučný, bezserifový atd.). Je to inspirováno praxí z původní ruční sazby. Dnes se k této myšlence některé OpenType fonty znovu vracejí a zavádějí feature „Optical size“. Jen to musejí písmomalíři pro každou velikost nakreslit zvlášť, zatímco Knuth vytvořil celkem zhruba 90 fontů rodiny Computer Modern vesměs ze společných parametrizovaných popisů znaků v Metafontu.
Zatímco v textové sazbě je opticky nejdůležitější účaří a střední dotažnice, v matematické sazbě je významná jiná vodorovná linka, která prochází středem znaků plus, mínus, je osou většiny operátorů a přesně půlí všechny závorky ve všech velikostech. Tato matematická osa je mírně výše než účaří a celý vzorec ji musí respektovat. Například v tomto vzorečku
$$ {\bi A} = {1\over2} \pmatrix {a&b&c\cr d&e&f} \cdot \pmatrix {x\cr y\cr z} $$
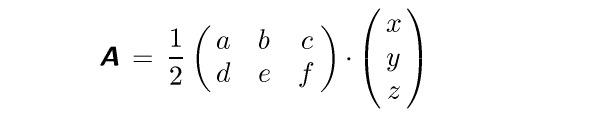
si spíše všimneme matematické osy (procházející rovnítkem, zlomkovou čarou a tečkou) než účaří. V matematickém fontu musí tedy být uložen metrický údaj o vzdálenosti matematické osy od účaří.
Kromě toho matematický font obsahuje čtrnáct dalších metrických údajů: posun exponentu nahoru ve volném (1) nebo stísněném režimu (2), posun indexu dolů, tloušťka zlomkové čáry, mezerování kolem zlomkové čáry, kolem velkých operátorů atd. V TeXooku v dodatku G je pak přesně popsáno, jak TeX s těmito metrickými údaji pracuje, aby vytvořil matematický vzorec. Uživatel to nepotřebuje vědět, mu stačí, že vzorec vypadá dobře.
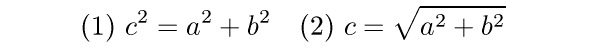
Pečlivý uživatel může vzorec dále doladit vkládáním různých dodatečných mezírek (kladných nebo záporných), ale není to obvyklé.
Vnořené závorky se v matematice rozlišují podle velikostí:
$$ \alpha \bigl(f(x)+f(y)\bigr) = f(\alpha x) + f(\alpha y) $$
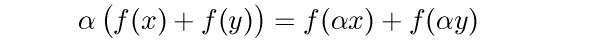
Závorky musejí také vždy na výšku obklopit výraz, který uzavírají. Ve zdrojovém
textu je nutné obklopovaný výraz vyznačit znaky \left...\right.
Například:
$$
\|f\| = \left(\int_0^1 f^2(x) {\rm d}x\right)^{1\over2},\quad
\left\|\sum_{i=1}^k f_i\right\| \leq \sum_{i=1}^k \|f_i\|.
$$
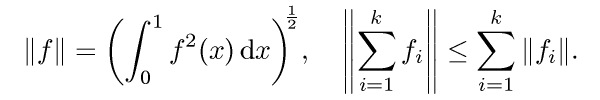
V matematické sadě fontů musí být připraven speciální font se zvětšovacími
objekty, jako jsou závorky různých druhů. Zvětšování není spojité, ale po
skocích. Ve fontu je sada připravených velikostí včetně komponentů, ze kterých
lze v případě potřeby poskládat závorku libovolné větší velikosti.
Jednotlivé velikosti jsou ve fontu vzájemně propojeny odkazy. TeX se po použití
\left...\right o výběr správné velikosti stará sám.
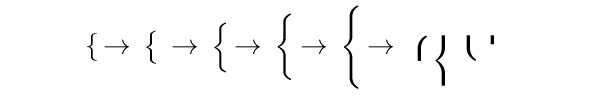
Kromě závorek jsou ve speciálním fontu připraveny různě velké znaky pro véčko odmocniny, přitom vodorovnou čáru TeX doplní automaticky dle šířky výrazu.
$$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1-x}}}}$$
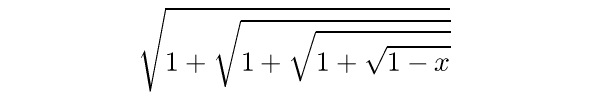
Konečně jsou v TeXu připraveny různé matematické akcenty, které mají možnost se pro změnu natahovat ve vodorovném směru.
$$
\overrightarrow{x+y} = \vec x + \vec y, \qquad
n^k = \underbrace{n\cdot n\cdots n}_{k\times}
$$
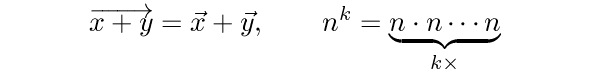
Někdy se matematik potřebuje rozšoupnout:
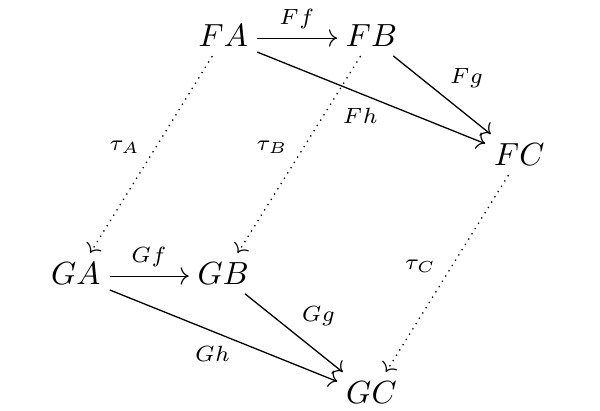
Tato poslední ukázka byla vytvořena pomocí makrobalíčku XYpic, pěkný návod vytvořil Aaron Lauda.
Proč je jednou použito slovo 'font', a jednou 'písmo'? Má to nějaké významové rozlišení?Font chápu jako písmo implementované v počítači. Pokud mluvím výhradně o počítačích (jako zde), je možné ta dvě slova brát jako synonyma a jejich střídání má pouze zvýšit pestrost při vyjadřování (to znáte ze slohových cvičení ze školy). Řez je varianta dané rodiny písma. Rodina se skládá z více řezů (variant), např. antikva, kurzíva, tučné. Chápu, že jsem nyní uvedl definici kruhem, ale snad si rozumíme.
 Skoda ze podobny plugin neni soucasti KDE Telepathy.
Dekuji autorovi za clanek.
Skoda ze podobny plugin neni soucasti KDE Telepathy.
Dekuji autorovi za clanek.
ISSN 1214-1267, (c) 1999-2007 Stickfish s.r.o.