Portál AbcLinuxu, 1. května 2025 22:34
V tomto seriálu se podíváme na schopnosti a možnosti využití GNU R.
GNU R (web projektu) je pro statistiku něčím podobným, čím je GIMP pro fotografie. Program se dá využít i bez hlubší znalosti statistiky na řešení jednoduchých praktických problémů.
Na Debianu a odvozených distribucích jako např. Ubuntu nainstalujeme
sudo apt-get install r-base
Na SuSE se balíček jmenuje také r-base. Na Redhatu a Fedoře R-core.
Ke zdrojovým kódům se dostaneme z domácí stránky -> CRAN -> Czech Republic -> nadpis Source Code for all Platform.
V příkazové řádce bashe zadáme velké R a naběhne nám interní příkazová řádka programu R. Je to něco jako shell, který občas otevře druhé grafické okno s nějakým grafem, ale funguje nadále, i když jsme okno s grafem ještě nezavřeli. Na zkoušku hned zadáme nějaký příkaz:
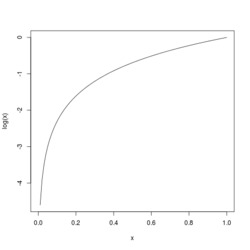
R plot(log)
Vytvoří se nám okno zobrazující graf funkce logaritmus. Co když chceme graf tisknout do PDF? Tak před tiskem grafu zadáme příkaz pdf() a po tisku (možná i více grafů) zadáme dev.off(), aby se graf(y) do PDF kompletně zapsal(y). Tisk půjde do souboru Rplots.pdf.
Chceme-li PNG, místo pdf() použijeme příkaz png(). Jméno souboru bude pak Rplot001.png atd., a každý graf půjde do separátního PNG.
Program R můžeme opustit pomocí CTRL-D nebo quit(). Zeptá se nás přitom, zda chceme uložit prostředí. V tom případě budeme moci používat všechny data a proměnné po opětovném startu tak, jak jsme je opustili. Můžeme si také přečíst o použitých funkcích:
help(log) help(plot)
R zvládne velikostně tak milióny položek seznamů, tabulek atd. Záleží samozřejmě od výpočetní obtížnosti operace. Pak se zavaří – teda spíš se zavaří nervy uživatele při čekání na doběhnutí operace. A totéž se stává při ukládání prostředí a jeho opětovném nahrávání při startu. Takže pokud se někde upíšeme o nulu, je třeba R killnout. Může se nám také podařit, že R se úplně odvaří, neboť se zavaří při každém startu, protože nahrává příliš velké prostředí. V tom případě smažeme soubor .RData v aktuálním adresáři.
Běžný člověk nedělá celý den nic jiného než že si tiskne grafy funkce logaritmus, to je jasné, tak si teď ukážeme něco, co snad může být prakticky užitečné.
Dejme tomu, že stavíme na chatě latrínu, kůlnu, altánek, sklep atd. a naskýtá se otázka, jak vysoké udělat dveře, aby prošli nejen členové rodiny, ale i případné návštěvy. Řekněme, že víme, že výška populace se řídí normálním rozložením. Tomu se říká také Gaussovo rozložení. Je to takový ten kopeček, jedna z nejčastějších distribucí. Vyskytuje se v případě, že měřená veličina je výsledek součtu množství nezávislých náhodných jevů. V našem případě množství genů a faktorů prostředí, které výšku ovlivňují. Řekněme že průměrná výška je 173 cm a směrodatná odchylka 6 cm a stanovíme si cíl, že 99% našich návštěv dveřmi projde. Jak vypočteme, jak vysoké dveře udělat?
x=180:200 plot(x,100*pnorm(x,mean=173,sd=6),ylim=c(98,100) ,ylab="Procent co projde dveřmi",xlab="výška dveří [cm]")
Vidíme, že je třeba 187 cm. Kdybysme ale zaokrouhlili na 190 cm, projde dveřmi už 399 ze 400 lidí.
Operátor dvojtečky vytváří sekvenci čísel od jednoho čísla k druhému s
krokem 1. pnorm je distribuční funkce normálního rozložení, také bychom to mohli
udělat s funkcí qnorm. Pomocí ylim a xlim se dá omezit číselný rozsah os,
např. když chceme graf zazoomovat na detail. A xlab a ylab jsou – překvapivě
– popisky os grafu.
qnorm je funkce kvantilová, což je distribuční funkce s prohozenými osami. Funkce pnorm a qnorm jsou dle mého názoru koncepčně velmi jednoduché. Funkci pnorm se dá výška v centimetrech a ona vrátí, kolik % populace tím projde. Nevrací ale procenta 0-100, ale zlomek 0-1. Funkci qnorm se řekne, kolik % lidí chceme, aby prošlo (zase, v rozsahu 0-1) a ona nám vrátí, jak vysoké dveře máme udělat.
Když jsme to už udělali s pnorm, s qnorm je to pak obdobné, stačí prohodit číselné rozsahy a popisky os. Takhle to vypadá s funkcí qnorm:
x=seq(0.98,1,by=0.001) par(lab=c(8,8,7)) plot(x*100,qnorm(x,mean=173,sd=6) ,xlab="Pravděpodobnost, že projde dveřmi [%]" ,ylab="Výška dveří [cm]",main="Stavíme dveře")
Zde jsem vyšperkoval graf hlavním nadpisem (main). Dále jsem zahustil stupnici na ose x i y pomocí příkazu par a jeho parametru lab. Více informací je v help(par). Tentokrát jsme místo dvojtečky použili funkci seq(), kde se dá specifikovat i krok parametrem by.
Pokud se ale nechceme zabývat tiskem grafů a zajímá nás jenom to jedno numero, uděláme to takhle:
> qnorm(0.99,mean=173,sd=6) [1] 186.9581
No a jak naše modelová distribuce výšek vypadá? Odvodil jsem ji z nějaké diplomky z tělesné výchovy, je ale principiálně špatně, protože ve skutečnosti jsou v populaci kopečky dva, jeden pro muže a druhý pro ženy. Dále se pak připočítává ještě 15-20 cm, aby průchod dveřmi nebyl psychicky traumatizujícím zážitkem, kdy člověk neví, zda si hlavu rozbije či ne. Na ukázku jsem ale použil tuhle zjednodušenou.
x=seq(150,200,by=0.1) plot(x,dnorm(x,mean=173,sd=6),type="l" ,main="Modelové rozložení výšek v populaci" ,xlab="Výška [cm]" ,ylab="Nekalibrovaná hustota pravděpodobnosti")
Jako další ukázku provedu histogram znaků v HTML zdrojáku. Takové histogramy se dají použít k určení typu souboru nebo druhu přirozeného či programovacího jazyka.
d=readBin(url("http://abclinuxu.cz","rb"),"integer",size=1,signed=FALSE,n=100000)
length(d)
hist(d)
Širší obrázek jsem udělal pomocí png(width=800). R nám vytiskne délku (94008) a objeví se nám rudimentární histogram, kde toho ale moc nevidíme, protože blízké ASCII znaky jsou shlukovány dohromady. Nastavíme proto, kde budou hranice mezi jednotlivými sloupečky histogramu:
hist(d,breaks=seq(-0.5,255.5),xlim=c(32,127) ,labels=sapply(as.raw(seq(0,255)),rawToChar) ,xlab="ASCII code",freq=FALSE)
Histogram mi dává smysl. Nejsilnější je mezera, která je typická pro texty v evropských jazycích. Dále nám tam trůní silné samohlásky aeio, a pak jsou silně zastoupené znaky typické pro použitý programovací jazyk HTML – špičaté závorky, rovnítko, lomítko, úvozovka.
breaks nastavují hranice sloupečků – včetně začátku prvního a konce posledního. xlim omezí na určitý rozsah znaků. labels jsou znaky, které jsou malovány nad sloupečky histogramu. freq přepne zobrazování četnosti v počtu znaků na zobrazování jako násobek celkového počtu znaků v dokumentu.
Funkce seq vyrábí sekvence čísel, s defaultním krokem 1. c je velmi často používaná funkce, která z několika čísel vytvoří seznam nebo spojí seznamy dohromady. funkce sapply aplikuje předepsanou funkci na prvky seznamu a z výsledku udělázase seznam. Kdyby tam sapply nebyla, z nějakého důvodu by to nevytvořilo seznam jednoznakových řetězců, ale jeden dlouhý řetězec.
Funkce hist je na kreslení histogramů. Manuálové stránky k ní pak jsou nejen pod jménem hist, ale i pod jménem plot.histogram (odkaz je v manuálové stránce hist). U více grafových funkcí je to tak, že další parametry jsou pod plot.něco. Další všeobecné parametry jsou pak pod plot.default a pod par(). Pokud chceme použít par(), zavoláme ho před tím příkazem, kterým něco malujeme.
28.8.2014 12:17
Ruža Becelin | skóre: 40
| blog: RuzaBecelinBlog
Program se dá využít i bez hlubší znalosti statistiky na řešení jednoduchých praktických problémů.to je tragedie dnesni doby, zrovna tak jako GIMP dela z lidi grafiky a HTML programatory. S hlubsimi znalostmi je clovek dnes jen pro smich. Priznavam , ze jsem se neudrzel a prosim, aby to nikdo nekomentoval.
Jeste me rozesmalo nasazeni pro stanoveni optimalni vysky dveri. Vetsi absurditu vytrzenou z reality jsem uz dlouhou necetl
"
2.9.2014 20:44
Václav "Darm" Novák | skóre: 26
| blog: Darmovy_kecy
| Bechyně / Praha
12.10.2014 13:46
Petr Tomášek | skóre: 39
| blog: Vejšplechty
30.8.2014 14:56
pools | skóre: 19
| blog: Svědek Damdogův
| Opava/Praha
12.10.2014 13:34
Petr Tomášek | skóre: 39
| blog: Vejšplechty
root@xxx:~# cat /etc/debian_version 7.6 root@xxx:~# apt-get install r-base Reading package lists... Done Building dependency tree Reading state information... Done Package r-base is not available, but is referred to by another package. This may mean that the package is missing, has been obsoleted, or is only available from another source E: Package 'r-base' has no installation candidate
12.10.2014 13:36
Petr Tomášek | skóre: 39
| blog: Vejšplechty
ISSN 1214-1267, (c) 1999-2007 Stickfish s.r.o.