Octave - 12 (měřítko os a speciální grafy)

19. 4. 2006 | Jiří Poláček

Články - Octave - 12 (měřítko os a speciální grafy)  

Pokračování článku o grafickém výstupu Octave se zaměřuje na vzhled os a popisuje vybrané speciální dvourozměrné grafy.

Měřítko os a popisky grafu

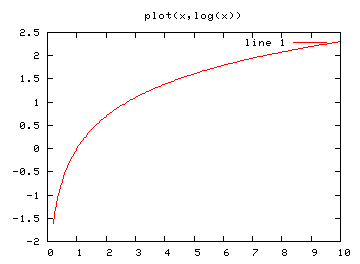
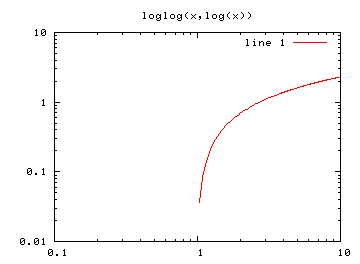
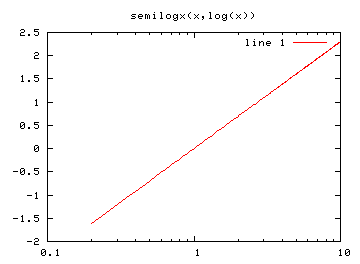
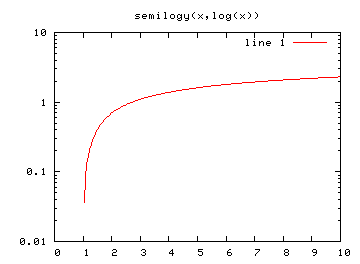
Příkaz plot popisovaný v minulém díle vykresluje grafy s lineárními osami. Funkce loglog, semilogx a semilogy mají stejné vstupní parametry, vykreslené grafy se však liší - jak již názvy napovídají - logaritmickým měřítkem os (buď oběma či pouze tou, která je uvedena v názvu):

>> x=linspace(0.2, 10, 200);
>> plot(x, log(x))
>> loglog(x, log(x))
>> semilogx(x, log(x))
>> semilogy(x, log(x))

Popisky nad grafem, jak jsou vidět na obrázcích, byly (a budou) doplněny funkcí title, například jako:

title('semilogx(x,log(x))')

Veškeré další požadavky týkající se os grafů směřují k použití funkce axis. Ta je dalším příkladem funkce s různorodým počtem parametrů. Volána bez jakéhokoliv parametru nastavuje měřítko os automaticky. Jedním z přípustných a zároveň volitelných parametrů může být dvou či čtyřprvkový vektor čísel (pro třírozměrné grafy i šestiprvkový), kde první dvě čísla udávají kraje osy x a druhá dvě čísla kraje osy y:

>> axis([-1, 10, -0.8, 0.8])
>> plot(x,sin(x))

Dalšími parametry funkce mohou být řetězce s následujícími účinky na osy grafu:

• přizpůsobení grafu velikosti výstupního zařízení (volby se vylučují, tj. pouze poslední uvedená bude platná):
  • 'square' - graf bude čtvercový bez ohledu na velikost výstupního zařízení
  • 'equal' - vzdálenosti na osách budou stejné bez ohledu na velikost výstupního zařízení
  • 'normal' - graf se přizpůsobí velikosti výstupního zařízení
• zobrazování čárek a hodnot na osách (pokud jsou zakázány čárky, nezobrazí se ani hodnoty):
  • 'on', 'off' - úplně zapne/vypne čárky a hodnoty
  • 'ticx', 'ticy' - zobrazí čárky pro zvolenou osu (a nezobrazí pro nezvolenou)
  • 'labelx', 'labely' - zobrazí hodnoty pro zvolenou osu (a nezobrazí pro nezvolenou)
  • 'nolabel' - schová hodnoty na obou osách
• pořadí hodnot na ose y:
  • 'xy' - v horní části grafu jsou vyšší hodnoty
  • 'ij' - v horní části gradu jsou nižší hodnoty

Nuže několik příkladů (příkazy psány ve skriptech):

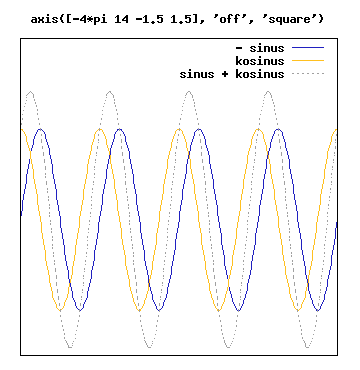
axis([-4*pi 4*pi -1.5 2], 'off', 'square');
x=linspace(-4*pi,4*pi,401);
plot(x,sin(x),'8;sinus;',x,cos(x),'9;kosinus;',x, sin(x)+cos(x), '0;sinus + kosinus;')

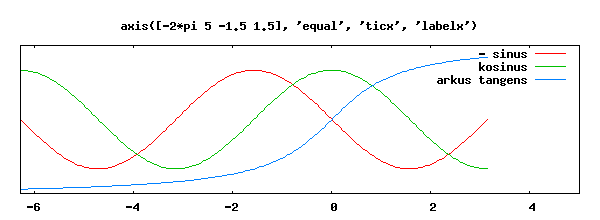
axis([-2*pi 5 -1.5 1.5], 'equal', 'ticx', 'labelx');
x=linspace(-2*pi,pi,201);
plot(x,-sin(x),';- sinus;',x,cos(x),';kosinus;',x, atan(x), ';arkus tangens;')

title('graf, kde je reverzní osa y a popisky os');
axis([-4*pi 4*pi -1.8 1.5], 'normal', 'ij', 'labely');
grid on; % vodící čáry
xlabel('toto je popisek osy x');
ylabel('toto je osa y');
x=linspace(-4*pi,4*pi,401);
plot(x, sin(x).*atan(x), '^m;sinus * arkus tangens;')

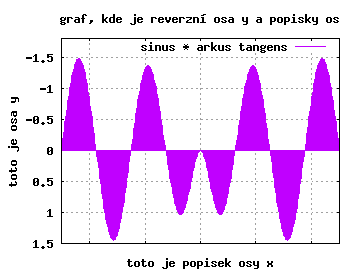
Poslední příklad také ukazuje, že vodicí čáry v grafu lze zapnout příkazem grid on a popisky jednotlivých os doplnit příkazy xlabel a ylabel.

Speciální dvourozměrné grafy

Pro vykreslování některých speciálních typů rovinných grafů můžeme v Octave sáhnout po funkcích na jejich vykreslování zvlášť určených. Jejich kompletní popis je v nápovědě, zde uvedeme pouze stručnější souhrn s příklady. Na vykreslování sloupcových a schodovitých grafů existují funkce bar a stairs:

hold on
x=linspace(-2,2,11);
bar(x, x.^2)
stairs(x, x.^2+1)

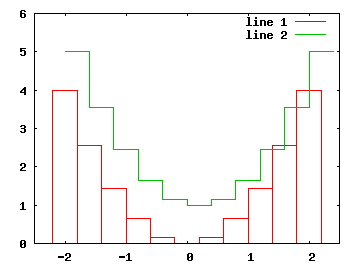
Všimněte si rozdílu, že sloupce jsou zobrazeny „na střed“ z vypočítané x-ové hodnoty, zatímco linie schodu začíná u spočítané hodnoty, jde vodorovně doprava a pokračuje nahoru či dolů k následující spočítané hodnotě - to vysvětluje, proč jsou v zobrazeném grafu schody posunuty kousek doprava oproti sloupcům.

Ani jedna těchto funkcí neumožňuje zadat třetí volitelný parametr pro definici stylu čáry. Lze však požadovat výsledek funkce jako dvouprvkový vektor souřadnic, které lze předat funkci plot s plnou parádou:

[barx, bary] = bar(x, x.^2)
plot(barx, bary, 'm;sloupce;')

Jiným typem sloupcového grafu je histogram - funkce se jmenuje hist. Algoritmus se snaží hodnoty ze vstupního vektoru (první parametr funkce) rozdělit do několika přihrádek (druhý parametr), výšky sloupečků ve výsledném grafu pak odpovídají počtu prvků v jednotlivých přihrádkách:

hold on
axis([0.5 5 0 4.5])
hist([1 1 2 3 3 3 4], 4)
hist([1 1 2 3 3 3 4], 2)

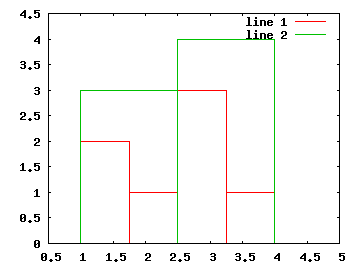
Čtyři červené sloupečky v grafu odpovídají čtyřem přihrádkám z prvního volání funkce hist, výsledek odpovídá tomu, že na vstupu jsou dvě jedničky, jedna dvojka, tři trojky a jedna čtyřka. V druhém případě dělíme jen do dvou přihrádek, proto zelené sloupečky sčítají jedničky s dvojkami a trojky se čtyřkami.

Histogram nám může být užitečný, když chceme vidět rozložení náhodných čísel z desetitisícového vzorku; čísla v příkladě sdružíme v pětisetinových intervalech:

>> hist(rand(1, 10000), 20, 100)

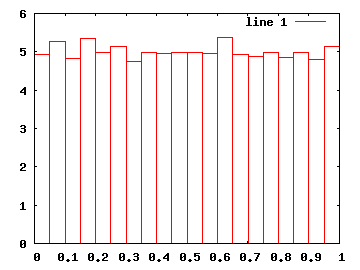
Třetí parametr slouží k normalizaci histogramu, jeho hodnota má ve výsledku být součtem hodnot jednotlivých sloupečků grafu. Zde zadaná hodnota 100 nám tedy zajistí, že hodnoty z osy y můžeme číst jako procenta.

Máme-li vykreslit graf z polárních souřadnic (tj. známe úhel a vzdálenost od počátku), pomůže nám funkce polar:

hold on
x=linspace(0,8*pi,361);
y=linspace(0,2,361);
polar(x,y, 'b;spirála;')
polar(x, 2*sin(2*x), ';2 * sinus 2x;')

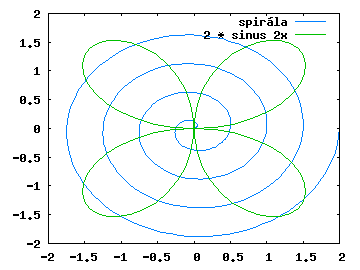
Nakonec se zmíníme o grafu s chybovými úsečkami. Základní funkce pro lineární souřadnice se jmenuje errorbar, existují však i další varianty pro logaritmická měřítka souřadnic. Nejjednodušší použití spočívá v poskytnutí třetího vektoru chyb ke každému vykreslovanému bodu - chyba se pak zobrazí jako rozptylová úsečka:

>> x=linspace(0,2*pi,41);
>> chyby=rand(1,41)*0.3;
>> errorbar(x,sin(x),chyby)

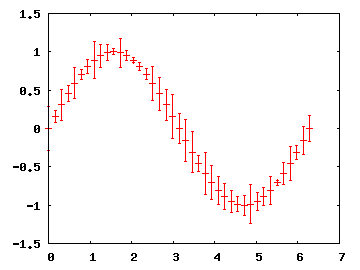
Chyba může být znázorněna také jako vodorovná úsečka či adekvátně široký sloupeček, v úvahu připadají i různé kombinace - více opět viz webový manuál.

Seriál Octave (dílů: 16)

První díl: Octave - 1 (je to kalkulačka), poslední díl: Octave - 16 (a co dál?).
Předchozí díl: Octave - 11 (kreslíme grafy)
Následující díl: Octave - 13 (dokončení grafiky)

Diskuse k tomuto článku