Octave - 11 (kreslíme grafy)

5. 4. 2006 | Jiří Poláček | Programování | 14750×

Jak Octave řeší grafický výstup, princip vykreslování čáry a kterak nastavit barvy, styly a legendu.

Jak Octave řeší grafický výstup

Octave ve snaze podobat se co nejvíce Matlabu obsahuje také podporu pro grafický výstup (ve smyslu kreslení matematických grafů). Samo o sobě však Octave grafy kreslit neumí - pro tento účel využívá program gnuplot (který je tudíž třeba mít v systému nainstalován). Z jistého úhlu pohledu by se dalo říci, že Octave funguje jako překladač kreslících funkcí z Matlabu do gnuplotu - jedním dechem je však nutno dodat, že se jedná o překladač velmi omezený, který zvládá jenom pár základních příkazů a nastavení. Pro plné využití všech možností gnuplotu máme v Octave k dispozici „nízkoúrovňové funkce“, díky kterým můžeme psát přímo příkazy gnuplotu nad daty z Octave. Následující texty se však budou zabývat především příkazy kompatibilními s Matlabem.

Jak se kreslí čára

Základní princip kreslení dvourozměrných grafů spočívá v zadání souřadnic bodů v kartézské soustavě - Octave vždy dva sousední body spojí úsečkou. Souřadnice bodů se zadávají jako dva vektory, jeden pro x-ové souřadnice a druhý pro y-ové; tyto dva (oba řádkové nebo oba sloupcové, ale hlavně stejně dlouhé) vektory pak figurují jako parametry funkce plot, která zajistí již samotné vykreslení grafu.

Příklad - vytvořme ze čtyř bodů A[0,4], B[5,-2], C[1,-3] a D[3,8] lomenou čáru tak, že bod A bude spojen s bodem B, bod B spojen s bodem C a konečně také bod C spojen s bodem D:

>> x=[0 5 1 3]; y=[4 -2 -3 8];
>> plot(x,y)

Mělo by se nám otevřít grafické okno gnuplotu vypadající podobně jako na následujícím obrázku:

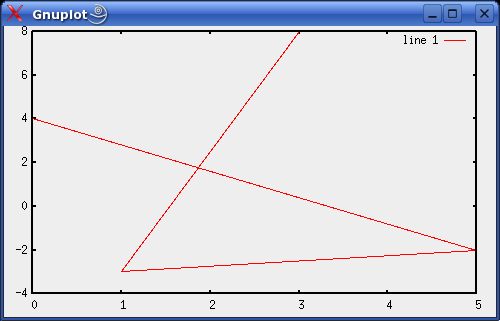
Vektor x postupně obsahuje x-ové souřadnice zadaných bodů, stejně tak vektor y obsahuje ve stejném pořadí y-ové souřadnice těch stejných bodů. Při vykreslování jsou pak sousední body spojeny úsečkou (tj. vykreslí se mezi nimi rovná čára). Pokud bychom chtěli zajistit, aby byl úsečkou spojen každý bod s každým, musíme to odpovídajícím způsobem zajistit v souřadnicových vektorech:

>> A=[0 4]; B=[5 -2]; C=[1 -3]; D=[3 8]; body=[A;B;C;D;A;C;B;D];
>> plot(body(:,1),body(:,2))

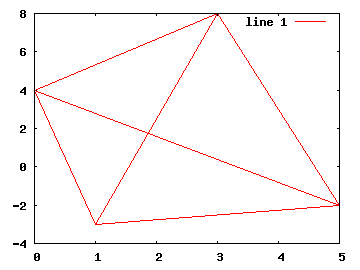
V grafu si také můžeme všimnout, že se automaticky nastaví měřítko grafu, vypíší hodnoty na osách a legenda grafu.

Hned na prvních příkladech tedy vidíme, že výsledné grafy nemusí být těmi správnými grafy z hlediska matematické analýzy, i když právě ty nejspíš budeme chtít ve výsledku vidět. Efektu hladké křivky dosáhneme prostě tím, že spočítáme dostatečný počet souřadnic vykreslovaných bodů. Porovnejte sinusoidu vykreslenou z 11 a 201 bodů:

>> x10=0:pi/5:2*pi;
>> plot(x10,sin(x10))
>> % versus
>> x200=0:pi/100:2*pi;
>> plot(x200,sin(x200))

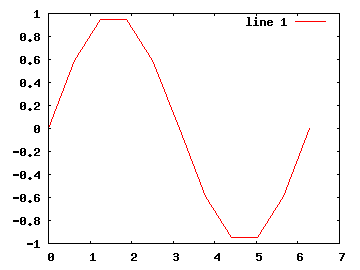
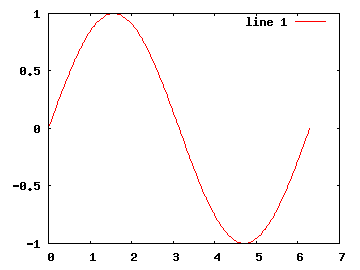
Uvědomme si u funkce sinus, že se počítá pro každý prvek vektoru x-ových souřadnic, čímž získáváme stejně dlouhý vektor y-ových souřadnic. Abychom si ušetřili čas s vymýšlením formule pro vektor lineárně rozložených x-ových souřadnic, můžeme používat funkci linspace, které zadáme dolní mez, horní mez a počet prvků výsledného vektoru:

>> linspace(0,10,4)
ans =
   0.00000   3.33333   6.66667  10.00000

Více grafů, více barev

Ve výchozím nastavení každé volání příkazu plot inicializuje výstupní zařízení, tj. smaže případný obsah z předchozích kreslících výstupů. Pokud chceme do grafu „přikreslovat“, nabízí se nám v podstatě dvě možnosti, které můžeme libovolně kombinovat. V prvé řadě můžeme podržet aktuální obsah výstupního zařízení s pomocí funkce hold. Volána s parametrem on tuto vlastnost zapíná, off značí výchozí stav mazání a konečně volání této funkce bez parametru přepíná z jednoho stavu do druhého. V jakém stavu se teď nacházíme, zjistíme funkcí ishold:

>> plot(x,sin(x))
>> ishold
ans = 0
>> hold on
>> plot(x,cos(x))
>> hold off

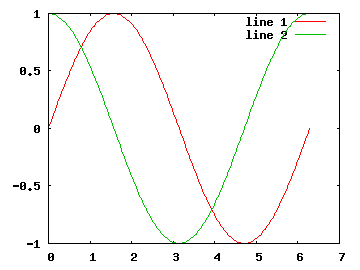
Druhou možností je zadání všech grafů do jediného příkazu plot, který může mít variabilní počet parametrů:

>> plot(x,sin(x),x,cos(x))

Přesněji řečeno, funkce plot může zpracovat libovolný počet dvojic x-ových a y-ových souřadnic. Navíc za každou touto dvojicí může následovat třetí volitelný řetězcový parametr, který upřesňuje barvu a styl čáry, respektive popisek k ní. Začněme ilustračním příkladem:

>> plot(0:5,5:-1:0,'^',0:6,6:-1:0,'Lm ',0:8,8:-1:0,'g*;popisek;' , \
0:.1:9,9:-.1:0,'.3',1:10,9:-1:0,'-@78',2 :10,9:-1:1,'c;usecka;')

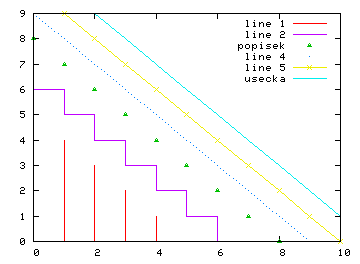
Za pomoci čísel, významových znaků a textů mezi středníky tak můžeme u každé vykreslované čáry určit:

• typ grafu: čárový (výchozí) - -, tečkovaný - ., schodovitý - L, nebo vynášecí - ^
• barvu určenou buď písmenem nebo číslem: r, g, b, m, c nebo w s příslušnými čísly 1-6, tj. v uvedeném pořadí červená, zelená, modrá, purpurová, azurová a bílá. Pokusy nasvědčují tomu, že i číslům 7-9 nějaké barvy přísluší.
• bodový graf: buď přímo uvedením symbolu, který se má v daném bodě vykreslit - *, +, o, x, nebo číselně s tím, že v takovém případě je nutno uvést dvojciferné číslo - první cifra určuje barvu a druhá cifra symbol (opět lze experimentovat s čísly 1-9). V případě, že chceme bodový graf, měli bychom uvést, zda body mají - -@ nebo nemají - @ (výchozí předpoklad) být spojeny čarou.
• popisek: uvádí se mezi středníky, například ;popisek;, středník na konci popisku nesmí chybět. Výchozí popisek zní „line“ plus pořadové číslo.

Obecně nezáleží na pořadí, v jakém se znaky zapíší, přesto to chce trochu experimentovat a nebýt překvapen, že kupříkladu číselná reprezentace barev může na každém výstupním zařízení znamenat něco jiného.

Příští povídání o Octave bude s grafy pokračovat, konkrétně se zaměří na měřítko os, popisky ke grafům a speciální dvourozměrné grafy.

       

Komentáře

[GeBu]

Znamená něco příkaz: "% versus", který je v textu v příkladu sinusovek s různou kvalitou?

[Jiří Poláček]

znak % uvozuje komentář

[GeBu]

Ve Windows verzi mi nefunguje "hold on" :(
parse error:
>>> hold on
^
>> hold on
parse error:
>>> hold on

[Jiří Poláček]

Vyzkoušel jsem teď tento příkaz ve windowsových verzích 2.1.36, 2.1.50 a 2.1.73 stažených z octave.sf.net a všude mi příkaz "hold on" bez problémů funguje. Vzhledem k tomu, že za příkazem hold se očekává textový parametr, zkuste hold 'on'.

[GeBu]

Ty apostrofy zabraly. Děkuji za obě odpovědi.

[asym]

V gnuplotu mi jde v pohode mysi rotovat 3D graf. Kdyz je ale volan z octave, tak to nejde. Jak je to mozne?

[Jiří Poláček]

V případě vzdáleného volání gnuplotu z Octave není inicializována myš. Příkaz gset mouse před vyreslením grafu tuto nepříjemnost napraví.

[asym]

nepomaha ani

__gnuplot_set__ mouse