Hra s písmenky - wxMaxima

18. 5. 2006 | Mark Stopka | Programování | 9940×

wxMaxima je volně šiřitelná aplikace, která slouží k práci s algebraickou matematikou. Je to grafická nadstavba nad aplikaci Maxima, která je napsána v Lispu.

Poznámka redakce: Článek vyšel ve dvou dílech v blogu m4r3k. V této úpravě vychází se souhlasem autora.

Maxima je včetně své grafické nadstavby součástí snad většiny distribucí GNU/Linuxu - ať už v oficiálních nebo neoficiálních balíčkových repozitářích. Pokud si přejete používat wxMaximu na Mac OS X, MS Windows, nebo vaše distribuce nepatří k většině, pak vás odkáži na domovskou stránky tohoto projektu (wxmaxima.sourceforge.net), kde jsou k dispozici rpm balíčky, deb balíčky, instalátor pro Windows a zdrojové kódy. Pro lepší představu o tom, jak tato aplikace vypadá, přikládám jeden screenshot

Základem wxMaximy je příkazový řádek, do kterého se vepisují jednotlivé příkazy. Některé funkce lze provést pomocí grafických klikátek, avšak ne všechny.

Heeelp!! (Nápověda)

Vestavěná nápověda ve wxMaximě je velice propracovaná. Dá se vyvolat pomocí klávesy "F1" nebo přes menu "Help/Maxima help". Integrovaná nápověda podporuje hledání a klíčové výrazy jsou poměrně intuitivní. Nápověda je rozdělena na dva základní celky: Manuál Maximy (Maxima Manual), který popisuje jednotlivé funkce, operátory a konstanty, a Úvod do Maximy (Introduction to Maxima), který obsahuje pár základních instrukcí pro práci.

Základy

Základní schopností wxMaximy jsou úpravy lomených výrazů. Výraz lze zadat jednoduše, například pomocí příkazu:

(1/(sqrt(x)+1)-2*sqrt(x)/(x-1))*(x^(-1/2)-1)

Bohužel je zde jedna pro mě nepříjemná vlastnost: musím psát místo výrazu například "2x" výraz "2*x", na což často zapomínám, a u obzvláště dlouhých výrazů se pak místo s chybějícím znakem špatně hledá, i když Maxima přímo napíše, kde se jí něco nelíbí. Priorita jednotlivých operátorů je stejná jako v běžné aritmetice, takže jako první je mocnění zapsané povelem "^", nebo "**", 2. odmocniny se dají zapsat pomocí funkce sqrt(x), nebo jako x^(1/2). Poté následuje násobení zapsané znakem "*" a dělení pomocí znaku "/", nejnižší prioritu mají operace sčítání (+) a odečítání (-).

Zadávání čísel

Čísla lze samozřejmě v Maximě zadat běžným způsobem, jen u čísel s určitým desetinným rozvojem se místo čárky "," používá (jak je u většiny aplikací zvykem) tečka ".". Maximu lze použít i jako numerickou kalkulačku, avšak toto užití je značně neohrabané, protože musíme pro zobrazení každého výsledku napsat příkaz:

%, numer

kde znak % říká, že pracujeme s předchozím výstupem, a příkaz numer říká, že si přejeme reálnou číselnou hodnotu. Maxima umí také pracovat s čísly komplexními, která zadáváme v algebraickém tvaru příkazem:

a+b*%i

Konstanty

Wxmaxima obsahuje poměrně malé množství konstant. Jsou to:

Konstanty
Konstanta	Co vyjadřuje	Zápis v maximě
e	základ přirozeného logaritmu	%e
pí	číslo pí	%pi
i	imaginární jednotka	%i
Nepravda	hodnota 0 Booleovy algebry	false
Pravda	hodnota 1 Booleovy algebry	true
+ nekonečno	reálné kladné nekonečno	inf
nekonečno	komplexní nekonečno	infinity
- nekonečno	reálné záporné nekonečno	minf

Grafy

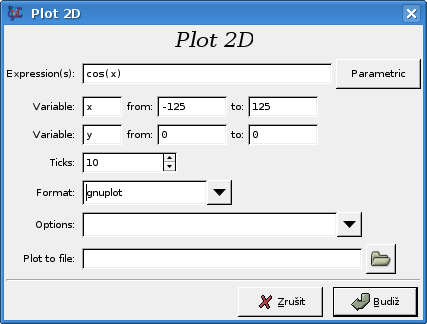
wxMaxima podporuje grafický výstup pomocí funkcí plot2d pro grafy dvourozměrné a analogicky plot3d pro třírozměrné grafy. wxMaxima neobsahuje žádný vlastní kreslící engine, ale umí ke spolupráci donutit gnuplot, nebo umí výstup podat ve značkovacím jazyce OpenMath. Nad obě tyto funkce existuje v programu wxMaxima grafické klikátko, které každému pomůže nakreslit graf libovolné funkce velice jednoduchým způsobem během pár vteřin. Ovšem pokud chcete nějaké specialitky, tak se zajisté pokusíte zkrotit příkaz plot2d, nebo jeho ekvivalent pro trojrozměrné grafy vlastními silami.

Kreslíme s klikátkem v rovině

Takže v prvé řadě si vysvětlíme jednotlivá pole v kreslícím formuláři. Pole s příhodným názvem Expression(s) slouží k zapsání předpisu funkce, jejíž graf si přejeme kreslit. Poté následují intervaly pro jednotlivé proměnné. Pokud si jen přejeme vidět, jak bude naše funkce vypadat při např. funkčních hodnotách 20 až 60, tak dosadíme vhodný interval za x tak, aby při tomto definičním oboru funkce těchto hodnot dosáhl. Následně si zvolíme vhodný obor hodnot, který si přejeme v grafu zobrazit; takže v našem příkladu třeba <20;60>. Dále následuje parametr ticks, který značí počet dosazovaných čísel ze zadaných intervalů pro výpočet funkční hodnoty.

Format značí, jaký budeme používat výstupní engine, a dává nám na výběr, zda to bude gnuplot nebo openmath. Gnuplot nám bez zadání dalších parametrů vykreslí graf na obrazovku; případně pokud zadáme cestu k souboru v políčku Plot to file, tak nám jej uloží do zadaného souboru v PostScriptu. Výstupní engine openmath nám bez parametrů vytvoří v domácím adresáři soubor s názvem maxout.openmath, který bude obsahovat souřadnice bodů tvořících tento graf zapsané ve značkovacím jazyce OpenMath.

Pokud nastavíme jako výstupní formát openmath a zároveň zadáme výstupní soubor, tak se jako vykreslovací engine použije gnuplot - a nám zase vznikne soubor obsahující graf ve formátu PostScript. Což je nejspíše nějaký bug. A v poslední řadě zde máme políčko options, v němž lze nastavit například mřížku, některou osu na logaritmickou a podobně. Ještě pomocí tlačítka Parametric můžeme vyjádřit funkci v parametrickém tvaru - zadáme předpis pomocí dvou předpisů: jeden platící pro souřadnice na ose x a druhý pro souřadnice na ose y se společným parametrem. Pokud chcete například více funkcí ve stejném grafu, tak je jednoduše zadáme obě do řádku Expression(s) oddělené pomocí čárky. A vznikne nám například příkaz:

plot2d([cos(x),sin(x),cos(x)*sin(x)], [x,-5,5])$

který nám nakreslí následující graf.

Grafy v třírozměrném prostoru

Stejně jako v případě příkazu plot2d existuje grafické klikátko i pro příkaz plot3d. Analogicky jako u kreslení dvojrozměrných grafů zde máme položku Expression(s), která slouží k zadání předpisu funkce, dále intervaly pro jednotlivé proměnné, poté nastavení mřížky, která je obdobou parametru ticks u dvojrozměrných grafů. Poté máme možnost opět zvolit výstupní formát, různé volby a kreslení do souboru.

Chybí volba Parametric, avšak parametrická funkce se jednoduše vytvoří zadáním jednotlivých předpisů oddělených čárkou. Například tímto příkazem:

plot3d([2+x*6,4+x*4,6+x*2], [x,-5,5], [y,-5,5])$

       

Komentáře

[Kníže Ignor]

ok, ale wxMaxima je jenom frontend, takže je podle mě divné říkat, že má nějaké konstanty atd.

[Kníže Ignor]

jinak mě taky trochu překvapil Möbiův list jako ilustrace k 3d grafům a pak suchý příklad... (člověk by skoro čekal příkaz, co ten M.l. vykreslí, že)

plot3d([cos(x)*(3+y*cos(x/2)), sin(x)*(3+y*cos(x/2)), y*sin(x/2)], [x,-%pi,%pi],[y,-1,1],['grid,40,15]);

[Heron]

Už během psaní článku jsem Markovi doporučoval, aby tam dal obrázek Calabiho-Yauovy variety (čtenáři knihy Elegantní vesmír jistě ví o čem mluvím). Marek místo 12 rozměrného objektu použil objekt jen s jednou stranou. Asi chtěl šetřit místem Vzorec tam dát mohl, máš pravdu.

[Kníže Ignor]

superstruny atd., to jo na to vás fyziky užije, ale udělat něco pořádnýho...

[Martin]

Ta knížka už mě dost dlouho láká a teorie superstrun jakbysmet. Mám to jako maturant ale šanci pochopit? Chci říct - vím, že je to populárně naučná kniha, ale to není vždy podmínkou pro to, že je to pochopitelné všem. Třeba knihy pana Stephena Hawkinga (které jsou napsány opravdu špičkově, si myslím) mě hodně bavily, ale po pravdě řečeno jsem se někdy taky dost ztrácel.

[Heron]

Upřímě řečeno, v tom se ztrácejí i doktoranti.

Einstein kdysi řekl, že teorii relativity rozumí dva lidé a nikdo neví, kdo je ten druhý.

O kvantovce nositelé nobelovy ceny říkají, že ji nerozumí vůbec nikdo.

Určitě doporučuji ji přečíst, nemusíte si ji kupovat, pučte si ji v knihovně a uvidíte.

Jak jste správně řekl, je to populárně naučná kniha, takže nepředpokládá moc znalostí z oboru. Na velmi jednoduchých příkladech (mravenci na hadici) je tam vysvětleno proč struny, jak vzniká svinutý rozměr a tak. V prvních kapitolách je vysvětlená teorie relativity stylem "Mach a Šebestová letí vesmírem". Překlad pana Motla je dobrý.

Poslední kapitoly (o M teorii) jsou skutečně hardcore.

[Kníže Ignor]

Já to četl, ale ani jsem si nevšiml, že to přeložil Luboš Motl! To bych měl k té knize hned jiný vztah. Mám od něj Pěstujeme lineární algebru, což je mimochodem také docela vtipná kniha.

Zvoliv^1 rozpravu o počtu tenzorovém za předmět poslední kapitoly, doufám, že se zavděčím čtenářstvu hojnému našemu a to tím více, že v naší mateřštině není mnoho spisů o tomto veledůležitém předmětu jednajících.

^1 Neprošlo jazykovou úpravou.

Taky bych chtěl být geniální jako Motl.

[Martin]

Teď si nějak nejsem jistý, jestli jsem ji u nás v knihovně opravdu náhodou neviděl. To bych byl pěknej trouba, že tady s tím otravuju. Jo, jsem trouba :o) Díky za odpověd, pustím se do ní třeba hned po matuře. Momentálně si čtu ve výjimečných chvílích volna Dialogy o matematice...

A to vykání není nutné, alespoň ve směru ostatní -> já, opačně se vždy přizpůsobím požadavkům dotyčného ;o)

[Bohumír Zámečník]

Elegantní vesmír byl moc pěkný, ale nedočetl jsem ho celý. Fraktály od Mandelbrota to samé. Před pár měsíci se mi velice líbila knížka Albert Lázslo Barabási: V pavučině sítí (o bezškálových sítích). No a teď o svaťáku si zpravuju chuť pokaženou z opakování češké gramatiky a slohu knížkou Algoritmy a programovací techniky od Pavla Töpfera. ;)

[Heron]

Pěkný článek, dobrý program na symbolické úpravy výrazu.

Dost mi připomíná dosový program Derive, nemá s ním maxima něco společného?

Nezná někdo dobrý matematický program, který obsahuje pokročilejší funkce pro zpracování signálů? FFT, filtry a pod? Moc by se mi to v těchto dnech hodilo.

[JaSel]

Co octave? Sekce 17.

[Heron]

Díky moc, to je ono!

Dokonce umí Hurstův koeficient. Mno, už vím co budu do večera dělat.

[Kyosuke]

Maxima je tak trošku dědeček, Derive je nejspíše mistrův učeň.

[srott]

Ako frontend maximy pouzivam texmacs, vyzorom je to dost podobne programu Maple

[Sinny]

Dobrý den, chtěl bych se zeptat, zda-li neznáte nějaký program pro analytické řešení integrálů a diferenciálních rovnic? Děkuji.

[Kyosuke]

A zkusil jsi Maximu?

[asym]

maple

[Radek Šlesinger]

... slouží k práci s algebraickou matematikou

Myslím, že se říká spíše "symbolické výpočty". Algebru bych do toho moc netahal.

[asym]

Symbolicke vypocty se daji delat jak v analyze, tak v algebre. Kazdopadne ale mate pravdu, ze je to presnejsi.

[Tomas]

Zdrávíčko mohl by mi nekdo napsat co delam spatne... pokud napisu do maximy nejak vyraz tak me to vyhodi cervene hlasku NOT CONNECTED TO MAXIMA dekuji.

[Adilkhatri]

검증된 파워볼사이트 를 찾으신다면 eos파워볼사이트 가 있는 파워볼사이트추천 에서 파워볼 을 즐기시길 바랍니다. 5년 이상 운영된 메이저업체 이며 지금까지 많은분들께 사랑받은 안전한파워볼사이트 입니다. 안전한파워볼사이트

[Adilkhatri]

You may remark on the request design of the blog. You should visit it's psyche boggling. Your blog review would swell up your guests. I was to an extraordinary degree satisfied to discover this site.I anticipated that would thank you for this incredible read!! 먹튀검증사이트