Octave - 15 (špetka matematiky)

22. 5. 2006 | Jiří Poláček | Programování | 10423×

Pár ukázek z praktické matematiky - čtyřstěn s pomocí vektorů, řešení rovnic a množinové funkce.

Čtyřstěn a trocha vektorové algebry

Pro seznámení s některými dalšími funkcemi Octave si vyřešíme následující příklad:

Funkci předáme souřadnice čtyř bodů v prostoru. Zkontrolujte, zda tyto body generují prostor a v kladném případě vykreslete čtyřstěn a spočítejte povrch čtyřstěnu.

Pro zjednodušení si odpustíme kontrolu počtu vstupních parametrů, tj. zda byly skutečně zadány čtyři tříprvkové vektory, a pustíme se do ověřování, zda body generují prostor:

function povrch=ctyrsten(A,B,C,D)
u=B-A; v=C-A; w=D-A;
if rank([u;v;w]) ~= 3
  error('Body negenerují prostor');
else

Z bodů si spočítáme tři vektory, které by měly být lineárně nezávislé, pokud mají generovat prostor. Funkce rank vrací hodnost matice, tj. počet lineárně nezávislých řádků této matice. Pokud tedy sestavíme matici ze spočítaných vektorů a hodnost takové matice bude menší jak tři, vektory jsou lineárně závislé a zadané body negenerují prostor. V opačném případě můžeme pokračovat:

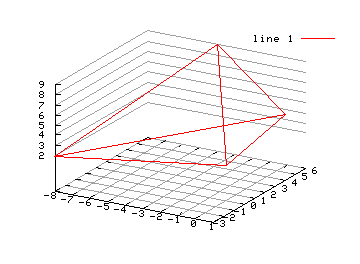
  M=[A;B;C;A;D;B;C;D];
  plot3(M(:,1), M(:,2), M(:,3));
  grid on

Souřadnice bodů jsou naskládány do matice tak, aby zde alespoň jednou každý bod sousedil s každým, funkce plot3 po té vykreslí čtyřstěn, sloupce matice M postupně tvoří x-ové, y-ové a z-ové souřadnice bodů. Příklad má v tomto bodě drobnou nedokonalost - funkce plot3 zatím není součástí oficiální distribuce Octave, lze ji najít v repozitáři doplňkových funkcí na octave.sourceforge.net (více o repozitáři v následujícím dílu).

  x=B-D; y=D-C; z=C-B;
  povrch=obtroj(u,v,z)+obtroj(u,w,x)+obtroj(v,w,y)+obtroj(x,y,z);
endif
endfunction

Dopočítáme zbylé vektory čtyřstěnu a spočítáme povrch jako součet obsahů jeho jednotlivých stěn.

Funkci obtroj pro výpočet obsahu trojúhelníka ze zadaných vektorů můžeme psát jak do dalšího souboru, tak do stávajícího ctyrsten.m ihned za definici hlavní funkce - tvoříme si tak vlastně lokální funkce:

function S=obtroj(va,vb,vc)
  a=norm(va); b=norm(vb); c=norm(vc);
  s=(a+b+c)/2;
  S=(s*(s-a)*(s-b)*(s-c))^(1/2);
endfunction

Obsah trojúhelníka počítáme podle Heronova vzorce z délek všech tří stran. Délky nám z příslušných vektorů (ve smyslu vektorové algebry, tj. chcete-li normu či magnitudu) spočítá funkce norm. Nuže zkušební volání naší funkce ctyrsten:

>> ctyrsten([1 4 5], [-4 6 9], [0 0 2], [-8 -3 2])
ans = 115.47
>> who
*** dynamically linked functions:
dispatch  max       svd
*** currently compiled functions:
__plt3__         ctyrsten:obtroj  isvector         strcmp
builtin:rank     grid             norm
columns          is_vector        plot3
ctyrsten         isstr            rows

Ve výpisu příkazu who si povšimněte položky ctyrsten:obtroj, která nás informuje, že v rámci funkce ctrysten byla také zkompilována lokální funkce obtroj.

Další funkce týkající se (stejně jako rank a norm) vektorové algebry jsou popsány v nápovědě. Nepřehlédněte dot a cross pro skalární a vektorový součin vektorů.

Řešení rovnic

Soustava lineárních rovnic

Pokud hledáme kořeny nějakého polynomu či soustavy lineárních rovnic, je určitě Octave vhodným řešitelem. Pokusme se najít například kořeny následující soustavy tří rovnic o třech neznámých:

-15a - 5b + 6c = -5
3a + 9b + 9c = 6
-8a + 5b + 12c = 7

Snad každý středoškolák ví, že takovéto příklady lze řešit přepsáním soustavy do matice a buď s pomocí Cramerova pravidla (a tedy počítáním determinantů) nebo úpravou matice do schodovitého tvaru získat kořeny soustavy. Ano, takto lze postupovat i v Octave, přičemž díky funkci det pro výpočet determinantu dané matice bude určitě první jmenovaný způsob jednodušší než programování převodu matice na schodovitý tvar, které jako triviální záležitost rozhodně označit nejde:

>> A=[-15 -5 6;3 9 9;-8 5 12];
>> B=[-5;6;7];
>> % Crammerovo pravidlo
>> for i=1:length(A) Ai=A; Ai(:,i)=B; x(i)=det(Ai)/det(A); end, x
x =
  -4.0000   7.0000  -5.0000

Nač si však komplikovat život. Pokud matici koeficientů označíme jako A, sloupcový vektor pravých stran jako B a sloupcový vektor kořenů jako X, pak platí A·X = B. Po úpravách dostáváme A^-1·A·X = A^-1·B, z čehož X = A \ B. Proměnné A a B jsme si již naplnili v předchozím příkladě, takže stačí jedno levostranné dělení:

>> X=A\B
X =
  -4.0000
   7.0000
  -5.0000

Polynomy

Pro hledání kořenů polynomu existuje v Octave funkce roots. Mějme například následující rovnici:

x⁵ − 4x⁴ − 55x³ + 10x² + 624x + 864 = 0

Její kořeny spočítáme následovně:

>> koeficienty=[1 -4 -55 10 624 864];
>> roots(koeficienty)
ans =
   9.0000
   4.0000
  -4.0000
  -3.0000
  -2.0000

Kontrolu správně opsaných koeficientů můžete udělat s pomocí funkce polyout, která vrací textovou reprezentaci polynomu ze zadaného vektoru:

>> polyout(koeficienty, 'x')
1*x^5 - 4*x^4 - 55*x^3 + 10*x^2 + 624*x^1 + 864

Samozřejmě můžeme chtít i opačnou operaci - z vektoru kořenů si nechat spočítat koeficienty polynomu, tato funkce se jmenuje poly:

>> poly([-4 -3 9 4 -2])
ans =
     1    -4   -55    10   624   864

Svým způsobem se jedná jen o roznásobení symbolického zápisu (x − x₁)(x − x₂) ... (x − x_n), takže když už jsme u toho násobení, je třeba zmínit funkci conv, která umí násobit dva polynomy. Chtějme vynásobit například (x² + 4x − 6)(5x + 4):

>> conv([1 4 -6],[5 4])
ans =
    5   24  -14  -24
>> [podil, zbytek] = deconv([5 24 -14 -24], [5 4])
podil =
   1   4  -6
zbytek =
  0  0  0  0

Jak je vidět z příkladu, funkce deconv provádí opak, tj. dělení polynomů.

K dalším užitečným funkcím pro práci s polynomy patří výpočet derivace či integrálu polynomu (funkce polyder a polyinteg), výpočet hodnoty polynomu v daných bodech (polyval) apod.

Množiny

Vektor lze chápat jako množinu, pokud neobsahuje žádné duplicitní prvky - tento požadavek splní funkce create_set (v Matlabu se tato funkce jmenuje unique):

>> v=[7 7 2 3 3 3 7 7 2];
>> mnozina=create_set(v)
mnozina =
  2  3  7

Zde je nutno podotknout, že v Octave existuje také funkce values řazená k funkcím popisné statistiky, která dělá totéž co create_set - s tím drobným rozdílem, že výsledkem je sloupcový vektor:

>> values(v)
ans =
  2
  3
  7

S množinami pak můžeme dělat jednoduché operace jako sjednocení, průnik a doplněk:

>> union([4 3 2 1],[2 4 6 8])
ans =
  1  2  3  4  6  8
>> intersection([4 3 2 1],[2 4 6 8])
ans =
  2  4
>> complement([4 3 2 1],[2 4 6 8])
ans =
  6  8

Můžete si povšimnout, že tyto funkce výsledky vrací setříděné od nejmenšího čísla po největší.

       

Komentáře

[Přemek Jordák]

Ještě bych doplnil, že pokud je soustava rovnic přeurčená, tzn. matice A ma více řádek než sloupců, potom octave při výpočtu pomocí backslash vrací hodnoty vyrovnané metodou nejmenších čtverců.

[Hynek (Pichi) Vychodil]

Proboha proč? Vždyť je to zbytečně výpočetně náročné a numericky nepřesné. Cramerovo pravidlo se hodí jen jako teoretický nástroj k důkazu některých vět, na specifické symbolické výpočty a numericky jen, když dostanu determinant "zadarmo". Pro numerické řešení prosím nikdy! I ten operátor dělení zleva je v matlabu, octave i jinde řešen Gaussovou eliminací s přeskládáním řádků.

[Jiří Poláček]

Nevidím nic špatného na použití Cramerova pravidla pro edukativní účely, ale je pravda, že jsem mohl zmínit, že řešení lineární soustavy dělením matic je mnohem vhodnější nejenom jednoduchostí zápisu, ale též výpočetní náročností.