Portál AbcLinuxu, 24. února 2026 05:47
Octave je volně šiřitelný klon Matlabu běžně dostupný jako balíček i pro vaši oblíbenou distribuci. K dispozici je i verze pro Windows. Následující text představuje první seznámení s tímto systémem pro práci s maticemi, který je zároveň programovacím jazykem podobným Pascalu.
Poznámka: Článek původně vyšel v blogu naopak.
Základním komunikačním prostředkem v Octave je příkazová řádka, do které
uživatel zapisuje své požadavky. V následujícím textu, zejména v
ukázkách, bude příkazový řádek signalizován znaky „>>“
(tzv. prompt příkazového řádku lze nejrůzněji měnit nastavením obsahu
proměnné PS1. Uvedený prompt získáme příkazem
PS1=">> ", více možností nastavení je popsáno v
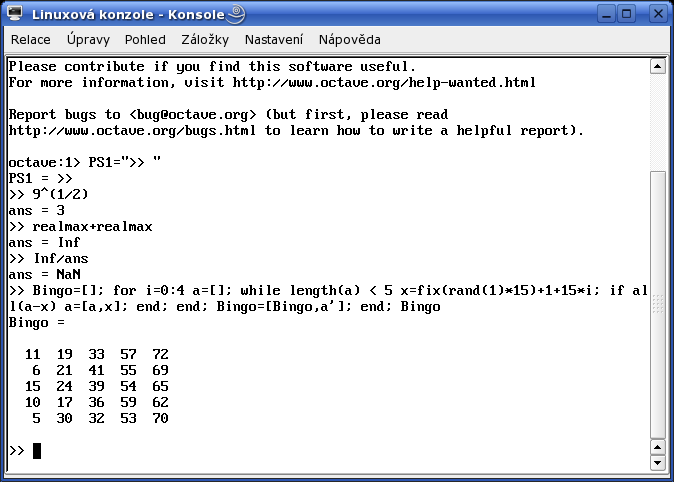
nápovědě programu). Jistou představu o popisovaném programu zajisté vyvolá
následující obrázek:
Vestavěnou nápovědu v Octave lze zobrazit pomocí příkazu help:
>> help
Na základě tohoto požadavku může program vypsat například následující text:
help is available for the topics listed below. Additional help for built-in functions, operators, and variables is available in the on-line version of the manual. Use the command `help -i topic' to search the manual index. Help and information about Octave is also available on the WWW at http://www.octave.org and via the help-octave@bevo.che.wisc.edu mailing list.
Podrobnější nápovědu k vestavěným funkcím a rezervovaným slovům je možné
vypsat příkazem help s odpovídajícím argumentem:
>> help fix
Jak sděluje úvodní text zabudované nápovědy, informace o Octave a další nápovědu je možné také získat na webových stránkách programu, konkrétně na adrese www.octave.org/doc.
Na té nejjednodušší úrovni lze Octave využít jako kalkulačku. Na příkazový řádek stačí zadat výraz, který se má spočítat. Po odeslání Octave vypíše výsledek:
>> 1+2*3 ans = 7 >> 4563*1.22 ans = 5566.9 >> (5-3)^2 ans = 4 >> 5**3 ans = 125
Aby bylo možné výraz vyhodnotit, musí samozřejmě být správně
zkonstruován. Při vyhodnocování má podle běžných pravidel aritmetiky
nejvyšší prioritu umocňování, pro které se používá znak „^“
(stříška) nebo dva těsně vedle sebe zapsané znaky hvězdička
„**“; následuje násobení „*“ a dělení
„/“; nejmenší prioritu mají sčítaní „+“ a odčítání
„-“. Následuje-li po sobě více operandů se stejnou prioritou,
vyhodnocuje se také obvyklým způsobem, tj. zleva doprava. Prioritu operandů
lze upravit pomocí kulatých závorek (pouze kulaté závorky; není možné zde
používat závorky hranaté [] a složené {}, ty Octave používá pro jiné
účely). Pro druhou odmocninu existuje v Octave funkce sqrt,
vhodnější však bývá použití umocňování na přepočítaný zlomek, tj.
sqrt(9) vrátí tentýž výsledek jako 9^(1/2).
Při práci s reálnými čísly se jako oddělovač celé a desetinné části používá podle amerických zvyklostí tečka, nikoliv čárka. Zapisujeme-li reálné číslo v absolutní hodnotě menší než 1, například 0,589, lze nulu z celé části vynechat:
>> -.25+.5 ans = 0.25000
Pro zápis typicky hodně velkých (respektive hodně malých) čísel se používá tzv. exponenciální tvar, tj. zápis s mocninou čísla deset. Například číslo 1,458 · 1045 se v Octave zapíše (a vypíše) jako 1.458e45, oddělovačem mezi základem čísla a exponentem tedy je písmeno e. Vězme také, že Octave umí pracovat s komplexními čísly:
>> (5+2i) * (1-j) ans = 7 - 3i
Písmena i a j v zápise mají stejnou hodnotu - znamenají imaginární jednotku a formálně v Octave figurují jako vestavěné konstanty, o kterých bude řeč dále.
Počet desetinných míst, který bude Octave zobrazovat u reálných čísel, se dá nastavit s pomocí příkazu format. Výchozí nastavení, které odpovídá parametru short, zobrazuje výsledek s pěti významnými ciframi, parametr long si vynutí 15 významných cifer a parametr bank zaokrouhluje na dvě desetinná místa:
>> r=sqrt(2); >> format short >> r r = 1.4142 >> format long >> r r = 1.41421356237310 >> format bank >> r r = 1.41
Existují ještě další parametry, které umožňují výpis čísel v binární či
hexadecimální podobě, vynucení si vědeckého zápisu s mantisou a další
speciality - viz help format.
Výsledek výpočtu si lze nejenom nechat zobrazit, ale také uložit do proměnné pro jeho pozdější využití. Proměnné v Octave vytváříme za chodu podle jejich potřeby, není nutné předem definovat jejich typ a velikost:
>> p=13 p = 13 >> P=12-6 P = 6
Předchozími dvěma příkazy byly vytvořeny dvě proměnné pojmenované
p a P. Vzhledem k tomu, že Octave rozlišuje malá a
velká písmena v názvech proměnných, jedná se o dvě různé proměnné. Do
proměnné p bylo přímo uloženo číslo 13, do proměnné P
pak výsledek výrazu 12-6. Stojí za povšimnutí, že výsledek výpočtu nyní
nezačíná „ans =“, ale názvem proměnné, do které jsme výsledek
uložili. Ono ans, které je možno chápat jako zkratku z
anglického answer – odpověď, v Octave funguje jako název
implicitní proměnné, do které se uloží každý poslední výsledek, u kterého
nebylo specifikováno, do jaké proměnné by se měl uložit. Necháme-li si nyní
vypsat obsah této proměnné, měli bychom dostat číslo 0,25 z příkladu
z předchozí sekce:
>> ans ans = 0.25000
Z příkladu je vidět, že aktuální obsah proměnné lze zjistit po odeslání jejího názvu. S vytvořenými proměnnými samozřejmě lze dále pracovat ve výrazech:
>> P+p ans = 19 >> ans^2 ans = 361
Seznam doposud uživatelem vytvořených proměnných zjistíme příkazem who:
>> who *** local user variables: P p
Vytvořenou proměnnou samozřejmě lze také zrušit, provádí se to příkazem clear následovaným seznamem proměnných, které se mají zrušit:
>> clear p P
Spuštění příkazu clear bez parametrů má za následek zrušení
všech proměnných.
Kromě proměnné ans obsahuje Octave po spuštění ještě celou řadu dalších speciálních proměnných (jejich seznam je uveden v nápovědě programu, mnohé z nich se týkají programového prostředí a mají vliv na správný běh Octave), z nichž některé plní úlohu konstant, například těch matematických, jako jsou Ludolfovo číslo π, Eulerovo číslo e (Matlab tuto konstantu ve svém repertoáru nemá) apod.:
>> pi pi = 3.1416 >> e e = 2.7183 >> i i = 0 + 1i >> j j = 0 + 1i >> realmin realmin = 2.2251e-308 >> realmax realmax = 1.7977e+308 >> realmax + realmax ans = Inf >> Inf/Inf ans = NaN
Konstanty i a j představují již zmiňovanou imaginární jednotku při práci s komplexními čísly; realmin ukazuje přesnost, s jakou je Octave schopno počítat; realmax nese hodnotu největšího čísla, s kterým je Octave schopno pracovat; Inf je vyjádřením nekonečna a konečně zkratka NaN znamená Not a Number - není číslo. Z uvedených příkladů je také vidět, kdy je možné poslední dvě jmenované konstanty získat jako výsledek výpočtu.
Je nanejvýš vhodné pro vlastní proměnné nepoužívat názvy těchto konstant, obzvláště v případech, že bychom jejich hodnoty potřebovali k výpočtu. Není totiž problém vytvořit si stejně pojmenovanou uživatelskou proměnnou:
>> pi=3+5 pi = 8
K původnímu obsahu konstanty se lze vrátit zrušením stejně pojmenované proměnné.
Stejně jako vědecké kalkulačky umí také Octave vracet funkční hodnoty běžných matematických funkcí, jako například:
>> sin(pi/2) ans = 1
Funkce se volají svým jménem, argument se uvádí za jménem v kulatých závorkách. Pokud je třeba počítat s mocninu dané funkce, v matematice zapsáno jako sin2 x, v Octave je toto třeba zapsat takto:
>> (sin(x))^2
Uveďme přehled základních funkcí, kterými Octave disponuje:
Přehled všech dostupných funkcí lze nalézt v nápovědě programu.
>> a=[1 2]; b=[3;4]; c=[5 6; 7 8]; >> a, b, c
ISSN 1214-1267, (c) 1999-2007 Stickfish s.r.o.