Pro testování byl vydán 4. snapshot Ubuntu 26.04 LTS (Resolute Raccoon).
Ben Sturmfels oznámil vydání MediaGoblinu 0.15.0. Přehled novinek v poznámkách k vydání. MediaGoblin (Wikipedie) je svobodná multimediální publikační platforma a decentralizovaná alternativa ke službám jako Flickr, YouTube, SoundCloud atd. Ukázka například na LibrePlanet.
TerminalPhone (png) je skript v Bashi pro push-to-talk hlasovou a textovou komunikaci přes Tor využívající .onion adresy.
Před dvěma lety zavedli operátoři ochranu proti podvrženým hovorům, kdy volající falšuje čísla anebo se vydává za někoho jiného. Nyní v roce 2026 blokují operátoři díky nasazeným technologiím v průměru 3 miliony pokusů o podvodný hovor měsíčně (tzn., že k propojení na zákazníka vůbec nedojde). Ochrana před tzv. spoofingem je pro zákazníky a zákaznice všech tří operátorů zdarma, ať už jde o mobilní čísla nebo pevné linky.
Společnost Meta (Facebook) předává React, React Native a související projekty jako JSX nadaci React Foundation patřící pod Linux Foundation. Zakládajícími členy React Foundation jsou Amazon, Callstack, Expo, Huawei, Meta, Microsoft, Software Mansion a Vercel.
Samsung na akci Galaxy Unpacked February 2026 (YouTube) představil své nové telefony Galaxy S26, S26+ a S26 Ultra a sluchátka Galaxy Buds4 a Buds4 Pro. Telefon Galaxy S26 Ultra má nový typ displeje (Privacy Display) chránící obsah na obrazovce před zvědavými pohledy (YouTube).
Byla vydána grafická knihovna Mesa 26.0.1 s podporou API OpenGL 4.6 a Vulkan 1.4. Je to první stabilní verze po 26.0.0, kde se novinky týkají mj. výkonu ray tracingu na GPU AMD a HoneyKrisp, implementace API Vulkan pro macOS.
Byla vydána nová verze 4.6 multiplatformního integrovaného vývojového prostředí (IDE) pro rychlý vývoj aplikaci (RAD) ve Free Pascalu Lazarus (Wikipedie). Využíván je Free Pascal Compiler (FPC) 3.2.2.
Byla vydána nová verze 3.23.0 FreeRDP, tj. svobodné implementace protokolu RDP (Remote Desktop Protocol). Opravuje 11 bezpečnostních chyb.
Španělský softwarový inženýr oznámil, že se mu podařilo na dálku ovládat sedm tisíc robotických vysavačů po celém světě. Upozornil tak na slabé kybernetické zabezpečení těchto technologií a jejich možné a snadné zneužití. Nesnažil se hacknout všechny robotické vysavače po světě, ale pouze propojil svůj nový DJI Romo vysavač se zařízením Playstation. Aplikace podle něj ihned začala komunikovat se všemi sedmi tisíci spotřebiči a on je
… více »Poznámka: Máte-li problém se zobrazováním znaku ∪ (∪), vyzkoušejte fonty DeJavu, které jej obsahují.
Jazyk, co to vlastně je jazyk? Základem takového jazyka je abeceda, což je jistá množina znaků specifická pro daný jazyk. Ze znaků abecedy jsou tvořena slova (pochopitelně neuvažujeme pro nás exotické jazyky typu japonštiny). Ty dále spojujeme do vět a to za pomoci gramatických pravidel. A právě gramatika je problémem. Jazyky, které se nazývají přirozené, mají gramatiky velmi složité, plné vyjímek a pro zpracování na počítačích se nehodí. Pokud mi nevěříte, tak se podívejte na diplomovou práci Johanky (ps, 1.0MB) a pokud budete rozumět alespoň slovům v obsahu, můžete se pustit do čtení (já, nemaje humanitní vzdělání, jsem skončil právě na něm). Nebo můžete navštívit přímo stránky Ústavu formální a aplikované lingvistiky na Matematicko fyzikální fakultě Univerzity Karlovy.
Druhou skupinou jazyků jsou formální jazyky. To jsou ty, jejichž pravidla pro generování a pohlcování jsou víceméně jednoduchá a deterministická (jednoznačná). Takové se potom hodí pro zpracování na počítačích. A o nich bude tento článek.
Teorie kolem formálních jazyků je rozsáhlá, ale pro potřeby článku se musí poněkud zkrátit. Jak jsem již napsal výše, základem jazyka je abeceda, kterou označujeme jako Σ (velké sigma) a Σ* (iterace), respektive Σ+ (pozitivní iterace) je množina konečných posloupností znaků z abecedy. Ty nazýváme slova na abecedou Σ a označujeme znakem w. Slovo, jehož délka je nulová, značíme e a pozitivní iterace tento znak neobsahuje. Jazyk L je potom podmnožinou množiny Σ*, respektive Σ+.
Ovšem jazyk je nutné nějakým způsobem popsat a právě zde nastupuje další pojem - gramatika. To je to, co známe i z přirozené řeči, a zde nám slouží ke konečnému popisu nekonečného jazyka. Každý formální jazyk tudíž musí mít specifikovanou nějakou gramatiku a při zpracování se mimo jiné ověřuje, zda jí zadaný vstup odpovídá.
Formálně je potom gramatika G čtveřice G=(N, Σ, P, S), kde
Důležitým pojmem je potom množina přepisovacích pravidel. Jedná se o podmnožinu kartézského součinu (N∪Σ)* N (N∪Σ)* × (N∪Σ)*. Přepisovací pravidlo je potom prvek (α,β)∈P a zapisuje se ve tvaru α→β.
Jazyk generovaný gramatikou je potom definován takto:
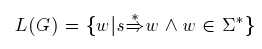
Je to množina slov w, které získáme derivacemi ze startovacího symbolu gramatiky. Symbol 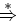 označuje reflexivní a tranzitivní uzávěr derivace. Pro nematematiky se jedná o postupné textové náhrady symbolů podle přepisovacích pravidel gramatiky. Zároveň musí být splněna podmínka, že slovo patří do množiny Σ*, tedy, že je tvořeno pouze symboly abecedy Σ.
označuje reflexivní a tranzitivní uzávěr derivace. Pro nematematiky se jedná o postupné textové náhrady symbolů podle přepisovacích pravidel gramatiky. Zároveň musí být splněna podmínka, že slovo patří do množiny Σ*, tedy, že je tvořeno pouze symboly abecedy Σ.
Důvody, proč jsem se tolik zabýval gramatikami a jejich formálním vyjádřením, jsou dva. Jednak je gramatika možnost, jak popsat potenciálně nekonečný jazyk konečným způsobem. A navíc tvar přepisovacích pravidel z množiny P umožňuje zařazení jazyka do některé z následujících čtyř tříd.
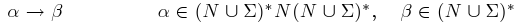
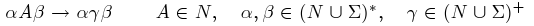
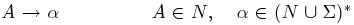
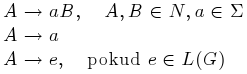
Přičemž jazyk generovaný gramatikou typu X se nazývá jazyk typu X a množina takových jazyků se značí LX. Platí 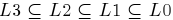 , což znamená, že množina regulárních jazyků je podmnožinou bezkontextových, ta zase podmnožinou kontextových a to celé je podmnožinou obecných jazyků. Podstatné na této klasifikaci je, že každá z výše uvedených tříd jazyků má jistou výpočetní sílu, přičemž čím vyšší třída, tím nižší síla.
, což znamená, že množina regulárních jazyků je podmnožinou bezkontextových, ta zase podmnožinou kontextových a to celé je podmnožinou obecných jazyků. Podstatné na této klasifikaci je, že každá z výše uvedených tříd jazyků má jistou výpočetní sílu, přičemž čím vyšší třída, tím nižší síla.
| Typ | Gramatika | Jazyk | Stroj |
| 0 | obecná | rekurzivně vyčíslitelný | Turingův stroj |
| 1 | kontextová | kontextový | Lineárně ohraničený TS |
| 2 | bezkontextová | bezkontextový | Zásobníkový automat |
| 3 | regulární | regulární | Konečný automat |
Tabulka udává jednotlivé typy gramatik, jazyky, které generuje a také minimální stroj, který dokáže načíst jejich věty. Rozdíl mezi pravou a levou regulární gramatikou je pouze v pozici nonterminálního symbolu B, obecně takové gramatiky nazýváme regulární.
Dost již bylo teorie. Představíme si gramatiky v praxi
. Mějme gramatiku G:
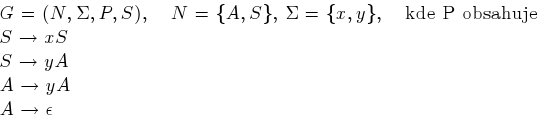
Příklad tvorby
věty jazyka generovaného touto gramatikou:
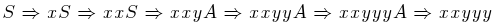
Na počátku byl startovací symbol gramatiky S. S využitím prvního pravidla jsme získali řetězec xS, další aplikací prvního pravidla jsme dostali xxS. Poté jsme aplikovali pravidlo číslo dvě a získali xxyS a s využitím dalších pravidel jsme nakonec vytvořili výsledné slovo xxyyy. Naše primitivní a jednoduchá gramatika ovšem umí
generovat i jiná slova, například y, xy, xyy, xxyy, xxxx...xxxy a tak dále. Pokud se podíváte pozorněji, tak mají daná slova něco společného. Dají se zapsat do regulárního výrazu x*y+, což značí, že na začátku může být žádné až nekonečně mnoho znaků x, které jsou následované alespoň jedním (ale i více) znaky y.
Co jsme to vlastně definovali za gramatiku? Pohledem na výše uvedenou klasifikaci gramatik zjišťujeme následující. První tři pravidla odpovídají prvnímu vzoru pro regulární gramatiky, protože S a A patří do množiny nonterminálních symbolů a x a y do množiny terminálních symbolů. A poslední pravidlo odpovídá třetímu vzoru pro regulární gramatiky. To znamená, že je naše gramatika regulární. Vyjadřovací síla regulárních gramatik, konečných automatů a regulárních výrazů naprosto stejná, proto je možné je navzájem zaměňovat. Nicméně regulární výrazy mají daleko kompaktnější zápis než gramatiky.
Na tomto místě si dovolím poznamenat, že spousta nástrojů svoje regulární výrazy vylepšovala do té míry, že přeskočili až do vyšších jazyků.
Regulární jazyky mají nejmenší vyjadřovací sílu. Ale pro spoustu problémů naprosto stačí a unixové regulární výrazy jsou toho jenom dokladem. Na druhou stranu by bylo vhodné mít něco
, co nám pomůže zjistit hranice regulárních gramatik. To něco se nazývá Pumping teorém (česky lemma o vkládání):
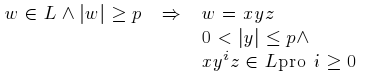
Daný vztah říká, že v dostatečně dlouhém slově w, které patří do jistého jazyka, můžeme nalézt tři části — x, y a z, přičemž nejdůležitější část y může zahrnovat i celé slovo. Poslední vztah potom značí, že část y můžeme z jazyka vyjmout, nebo jí libovolně zopakovat, a přitom stále zůstáváme v rámci stejného jazyka.
Díky této větě potom můžeme dokázat, že daný jazyk není regulární. Klasickým učebnicovým příkladem je například jazyk 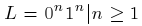 . Definice jazyka hovoří, že generuje stejný počet znaků a i b. Při hledání podřetězce y potom můžeme narazit na následující případy.
. Definice jazyka hovoří, že generuje stejný počet znaků a i b. Při hledání podřetězce y potom můžeme narazit na následující případy.
Protože nedokážeme najít žádný podřetězec y, dokázali jsme, že daný jazyk není regulární. To má i praktický význam, jelikož nemusíme hledat složité regulární výrazy na detekci takových řetězců, protože to prostě nejde. Na druhou stranu dokáží regulární jazyky vyřešit i některé problémy (bez důkazu)
Tento díl představoval lehký (velice lehký, zájemce odkazuji na přístupné materiály některých vysokých škol k této problematice) úvod do problematiky formálních jazyků. Tématem příštího dílu by měly být především regulární výrazy (ano i to je formálně podchyceno) a konečné automaty, protože k sobě spolu neodmyslitelně patří. Myslím, že na unixově založeném serveru se bude jednat o vděčné téma.
Toto je tak trochu experiment, protože se vymyká běžným tématům na ábíčku. Navíc obsahuje dost formálních náležitostí, a proto potřebuji vědět, jak se na to díváte po přečtení. Mám přidat, nebo raději ubrat? Těším se na vaše názory a na případné opravy chyb, které jsem napáchal.
Nástroje: Tisk bez diskuse
Tiskni
Sdílej:
![]()
![]()
![]()
![]()
![]()
![]()

A proč by abeceda (přirozeného jazyka) musela být univerzální? Jak může abeceda být jakkoliv univerzální? Nota bene prý z nějaké „podstaty“?Protože něco jako "abeceda jazyka" neexistuje. Existují různé abecedy, kterými se zapisují různé jazyky. Abeceda jako způsob označování jednotlivých hlásek či skupin hlásek, na která se dají rozložit jednotlivá slova, je univerzální proto, že vůbec není podstatné, jaký jazyk nějakou abecedou zapíšete. Ostatně většina nynějších kulturních jazyků používá více či méně upravenou tutéž abecedu (latinka, azbuka, řecké písmo, hebrejské, arabské, syrské písmo...), pouze v různém stádiu vývoje, a dá se poměrně dobře vystopovat, jak se nynější rozdílné znaky vyvíjely jeden z druhého. Japonská abeceda vznikla zase podobně zjednodušením čínských znaků, ale i tak je univerzální, protože na rozdíl od čínských logogramů se řídí výše popsaným principem abecedy, přiřazení znaků jednotlivým (nebo několika) hláskám, díky čemuž se dá japonskou abecedou psát i čeština, ostatně fonetické přepisy jmen či názvů v každém jazyce tuto univerzálnost abecedy dokazují názorně.



Myslím, že to bude nepochopení...existence grafémů je naprosto nepodstatná pro fakt, že slova jazyka (přirozeného i umělého) nejsou atomická, a to je IMO základní fakt, který se Michal snažil sdělit.A vidíte, já bych v tom viděl rozdíl mezi formálním a přirozeným (normálním) jazykem, že totiž přirozený jazyk můžeme zapsat abecedou teprve díky jeho (umělé) formalizaci (protipříklad viz čínština), zatímco autor od začátku aplikuje vlastnosti jazyků formálních i na přirozené (viz jeho zmínka o japonštině), s čímž si dovolím nesouhlasit (viz mou první reakci). Základem formálních jazyků tak může být "abeceda", jak píše autor, ale k přirozenému jazyku bylo naopak nutné "abecedu" (neboli vaši atomizaci) teprve vynalézt, což pak těžko označit jako jeho základ, díky němuž tento přirozený jazyk existuje (rozhodně přirozený jazyk nevzniká tak, že bychom skládali dohromady definovanou "abecedu" a tu teprve pak spojovali ve slova a věty, cesta je spíše opačná, od vět ke slovům a pak k jednotlivým hláskám či znakům abecedy). Proto mi tento úvod nepřijde jako vydařený a určitě by stál za upřesnění.

Tak, tak. Ona je abeceda k přirozenému jazyku něco jako přírodní zákon k přírodě. Model, který nám to umožní nějak uchopit, ale dost těžko to lze zaměňovat.Tak tak co? Reagujete na otázku: "Znamená to tedy, že morfémy bez formalizace v jazyku jako strukturální jev neexistují?" Odpověď tedy zní "ano, existují" nebo "ano, neexistují"? ;) Pokud definujete "abecedu" jako "jistou množinu znaků specifickou pro daný jazyk" (což není abeceda v běžném významu), proč používáte pojem "abeceda"? Jinými slovy, proč aplikujete na přirozený jazyk pojem jazyka formálního? Abeceda (přirazení značek abstrahizovaným hláskám, tedy poloze a činnosti mluvidel) se k přirozenému jazyku se právě rozhodně nemá jako přírodní zákon k přírodě. Protože abeceda nám vůbec neumožňuje přirozený jazyk pochopit (nemyslel jste gramatiku?). Je úplně lhostejné, jakou abecedou nějaký jazyk zapíšete, stále to bude tentýž jazyk.
Ostatně dobře je to vidět na tom, když zkusíte "českou latinkou" přečíst anglický text. Budete obtížně hledat angličana, který by Vám rozumněl.Maximálně bych mohl zkusit "českou latinkou" anglický text zapsat. Když ho přečtu (dekóduji znaky přiřazené určitým hláskám), bude to stále navzdory zápisu (podle vás) jinou abecedou anglický text, kterému každý Angličan bez problémů porozumí. Du jú andersténd? A vezmete-li si abecedu očištěnou od nánosů historie, tedy nějakou abecedu používanou k fonetickým přepisům jako je třeba fonetická abeceda IPA a naučíte-li se jí, můžete její pomocí zapsat text v jakémkoliv jazyce a když ho přečtete, bude vám jakýkoliv mluvčí jazyka rozumět, aniž byste použil něco, co odvážně nazýváte "množinou znaků specifickou pro daný jazyk". Na tom je naopak dobře vidět, co to znamená, že abeceda je univerzální.
Znamená to tedy, že morfémy bez formalizace v jazyku jako strukturální jev neexistují?Ne, znamená to, "že totiž přirozený jazyk můžeme zapsat abecedou teprve díky jeho (umělé) formalizaci". Což je obráceně než v jazyce formálním. Pokud vím, je řeč o abecedě, což je něco jiného než morfologie jazyka (a což jsem já ve svém příspěvku na rozdíl od vás definoval). Pokud si myslíte, že abeceda a morfémy jazyka jsou jedno a totéž, máte to říct, protože to vůbec není samozřejmost. A když je tedy řeč o morfémech jazyka, tak ty se neskládají z "abecedy" (znaků), ale naopak je lze zpátky vystopovat k původním lexémům. Znaky nejsou to, z čeho skládáme slova, naopak, slova (nebo chcete-li i vaše morfémy) díky abstrakci jednotlivých zvuků neboli hlásek (neboť jednotlivé hlásky nenesou žádný význam) můžeme na hlásky rozkládat. A ty teprve pak abecedou zaznamenat a je úplně lhostejné, jakou konkrétní podobou abecedy, neboť z abecedy se jazyk neskládá. Tím pádem nelze souhlasit s větami autora, pokud by je chtěl aplikovat na přirozený jazyk: Základem takového jazyka je abeceda [=jsou písmenka], což je jistá množina znaků [=písmenek] specifická pro daný jazyk. Ze znaků abecedy [=písmenek] jsou tvořena slova (pochopitelně neuvažujeme pro nás exotické jazyky typu japonštiny). Ty dále spojujeme do vět a to za pomoci gramatických pravidel. Základem jazyka nejsou písmenka, ani nejsou písmenka specifická pro nějaký jazyk, ani nejsou z písmenek tvořena slova. Pokud to vidíte jinak, např. že autor používá slovo "abeceda" nikoliv v běžném významu (čemuž ovšem odporuje jeho výslovná definice), např. metaforicky ve smyslu "abeceda lásky, abeceda linuxu" nebo snad dokonce "abeceda = souhrn morfémů", napište to. Klást jakoby významné otázky s podtextem, že polemizují s tím, co jsem napsal (a přitom se týkají něčeho úplně jiného), je velice jednoduchá strategie, jak diskusi zavést do slepé uličky.
Taky bych o tom mohl tak uvažovat, ale to bych pak rovnou mohl celou lingvistiku zahodit jako snahu násilně pasovat logiku na něco „tak krásně neformálně přírodního“...Samozřejmě můžete uvažovat třeba o růžových slonech... ale jak to souvisí s tématem diskuse (viz výše), budete muset osvětlit dříve, než bude možné na vaše úvahy nějak reagovat ;)
„Pokud to vidíte jinak, např. že autor používá slovo "abeceda" nikoliv v běžném významu (čemuž ovšem odporuje jeho výslovná definice), např. metaforicky ve smyslu "abeceda lásky, abeceda linuxu" nebo snad dokonce "abeceda = souhrn morfémů", napište to.“Que?
 Vždyť jsem se to o kus výše snažil sdělit a ještě jsem poukázal na teorii informace, kde prostě jiný termín pro atomické symboly zprávy není.
Vždyť jsem se to o kus výše snažil sdělit a ještě jsem poukázal na teorii informace, kde prostě jiný termín pro atomické symboly zprávy není.  Nebo o něm aspoň nevím.
Nebo o něm aspoň nevím.
Základem formálních jazyků tak může být "abeceda", jak píše autor, ale k přirozenému jazyku bylo naopak nutné "abecedu" (neboli vaši atomizaci) teprve vynalézt, což pak těžko označit jako jeho základ, díky němuž tento přirozený jazyk existuje (rozhodně přirozený jazyk nevzniká tak, že bychom skládali dohromady definovanou "abecedu" a tu teprve pak spojovali ve slova a věty, cesta je spíše opačná, od vět ke slovům a pak k jednotlivým hláskám či znakům abecedy).Jenže právě tohle je to, co tvrdí Chomsky, tedy, že i přirozené jazyky jsou tvořeny stejně jako formální jazyky svou abecedou a celým tímhle aparátem kolem. Jen je potřeba si uvědomit, že on netvrdí, že tou abecedou je abeceda písemného zápisu, ale určité myšlenkové elementy v mozku rodilého mluvčího. Tedy základem přirozeného jazykou je abeceda přirozených jazykových znaků a základem formálního jazyka je formální abeceda psaná. Na druhou stranu je fakt, že Chomskému například většina psychologů nemůže přijít na jméno a podobně. Otázkou je, jestli to nepramení právě z toho nepochopení, že abecedou u přirozených jazyků není písemná abeceda.
 ), ze srdce se smal a vypravel, jak kdyz byl on mlady student, jak to strasne zrali a mysleli, ze je to vrchol vseho
), ze srdce se smal a vypravel, jak kdyz byl on mlady student, jak to strasne zrali a mysleli, ze je to vrchol vseho 

Existují dvě skupiny objektových programátorů: Smalltalkeři, a ti, kteří to ještě nepochopili.Není to tak, že existuje jen jedna skupina? Smalltalkeři? :-P
 (Já na ty slovní hříčky jednou zajdu...
(Já na ty slovní hříčky jednou zajdu...  )
)

Mám přidat, nebo raději ubrat?tempo je docela silene, ale aspon to neni nudne a rozvlacne. co zaradit vic prikladu?
 . Potíž je v tom, že nedokážu přesně odhadnout, co můžu a co nemůžu vynechat, tak, aby tomu (s trochou snahy) rozumněl i člověk tímto nezasažený.
. Potíž je v tom, že nedokážu přesně odhadnout, co můžu a co nemůžu vynechat, tak, aby tomu (s trochou snahy) rozumněl i člověk tímto nezasažený.
 ) I ja jsem s tim mel problem... naopak jako skladacka nam to zacalo zapadat v okamziku, kdy jsme zacali psal prvni prekladace a dostali se k prakticke strance veci... (a uz jsem to za ty roky stacil opet uspesne pozapominat, protoze syntakticke parsery za mne delaji existujici implementace)
Ale mozna jsou nekteri vetsi snilci a takovyto stupen abstrakce jeste mozkove zvladaji levou zadni...
) I ja jsem s tim mel problem... naopak jako skladacka nam to zacalo zapadat v okamziku, kdy jsme zacali psal prvni prekladace a dostali se k prakticke strance veci... (a uz jsem to za ty roky stacil opet uspesne pozapominat, protoze syntakticke parsery za mne delaji existujici implementace)
Ale mozna jsou nekteri vetsi snilci a takovyto stupen abstrakce jeste mozkove zvladaji levou zadni...


 Ale simple prekladac javy jakozto seminarka nebo simulator vysoce pararelniho stroje jsme zvladli...
Ale simple prekladac javy jakozto seminarka nebo simulator vysoce pararelniho stroje jsme zvladli...
 ), vychrlil bych ze sebe, jak je ostatně mým dobrým zvykem, dlouhou řadu nadávek a vulgarismů.
Nikdy nejde snažit se psát populárně a zároveň se snažit být formální!!! V článku jsou nepřesnosti, je to samozřejmě daň populárnosti a omezeného prostoru pro článek.
Například tvrzení "A navíc tvar přepisovacích pravidel z množiny P umožňuje zařazení jazyka do některé z následujících čtyř tříd." čtenáře musí zmást (lze chápat buď tak, že neříká zhola nic - to díky slovu "umožňuje", nebo špatně). Většinový čtenář se z něho získá mylný dojem, že pravidla musí být vždy v tom "kanonickém" tvaru. Kam asi čtenář s využítím zmíněné věty zařadí gramatiku A -> aBC, B -> a, C -> a?
Dál si myslím, že by bylo třeba alespoň říct, že v té hierarchii jde vždy o vlastní podmnožiny.
Článek nesmí být nikdy pouze šikovným a smysluplným poskládáním poznatků ze skript/manuálu, musí v něm být vždy něco z autora. Nicméně toto je seriál, autor má ještě šanci se předvést. Do zvěřejnění dalšího dílu zůstanu zděšen
), vychrlil bych ze sebe, jak je ostatně mým dobrým zvykem, dlouhou řadu nadávek a vulgarismů.
Nikdy nejde snažit se psát populárně a zároveň se snažit být formální!!! V článku jsou nepřesnosti, je to samozřejmě daň populárnosti a omezeného prostoru pro článek.
Například tvrzení "A navíc tvar přepisovacích pravidel z množiny P umožňuje zařazení jazyka do některé z následujících čtyř tříd." čtenáře musí zmást (lze chápat buď tak, že neříká zhola nic - to díky slovu "umožňuje", nebo špatně). Většinový čtenář se z něho získá mylný dojem, že pravidla musí být vždy v tom "kanonickém" tvaru. Kam asi čtenář s využítím zmíněné věty zařadí gramatiku A -> aBC, B -> a, C -> a?
Dál si myslím, že by bylo třeba alespoň říct, že v té hierarchii jde vždy o vlastní podmnožiny.
Článek nesmí být nikdy pouze šikovným a smysluplným poskládáním poznatků ze skript/manuálu, musí v něm být vždy něco z autora. Nicméně toto je seriál, autor má ještě šanci se předvést. Do zvěřejnění dalšího dílu zůstanu zděšen 


 Lebo toto je podľa mňa presne to, čo článku chýba, komentár od niekoho, kto má chuť učiť sa, ale tento predmet nepozná.
Lebo toto je podľa mňa presne to, čo článku chýba, komentár od niekoho, kto má chuť učiť sa, ale tento predmet nepozná.
 Dotaz 2: Hotové slová musia patriť do iterácie abecedy. Teda posledným krokom musí byť pravidlo, ktoré na pravej strane nemá neterminál. Neterminály ako také nie sú pre jazyk vôbec podstatné, lebo, ako je aj uvedené v článku, spôsob tvorby jazykov pomocou je ekvivaletný rôznym strojom, ktoré hovoria, či slovo do jazyka patrí, alebo nie. Teda, dôležitá je len abeceda a pravidlá. To je koniec koncov celkom zrejmé, lebo je jedno, či máte rovnicu s neznámymi x, y, z alebo a, b, c, výsledok závisí na jej tvare; neformálne povedané. Dúfam, že to nevysvetľujem veľmi mätúco
Dotaz 2: Hotové slová musia patriť do iterácie abecedy. Teda posledným krokom musí byť pravidlo, ktoré na pravej strane nemá neterminál. Neterminály ako také nie sú pre jazyk vôbec podstatné, lebo, ako je aj uvedené v článku, spôsob tvorby jazykov pomocou je ekvivaletný rôznym strojom, ktoré hovoria, či slovo do jazyka patrí, alebo nie. Teda, dôležitá je len abeceda a pravidlá. To je koniec koncov celkom zrejmé, lebo je jedno, či máte rovnicu s neznámymi x, y, z alebo a, b, c, výsledok závisí na jej tvare; neformálne povedané. Dúfam, že to nevysvetľujem veľmi mätúco 
Slovo, jehož délka je nulová, značíme e a pozitivní iterace tento znak neobsahujemyslim, ze to nie je celkom presne. Ak Σ neobsahuje \E(epsilon-prazdne slovo) potom pozitivna iteracia tento znak neobsahuje. Ak vsak Σ obsahuje \E potom ho obsahuje ak pozitivna iteracia...aspon dufam, ze je to tak :)