TeX – 10 (příklad na vytvoření karetní hry)

4. 2. 2014 | Petr Olšák | Různé | 5340×

V minulém díle seriálu jsme si ukázali, že TeX se nebojí grafiky, dokonce naopak: pomocí TeXových maker lze grafiku řídit. Toto téma dnes uzavřeme podrobně komentovaným příkladem, kterým vytvoříme karetní hru Set. Příklad ilustruje nejen použití grafiky, ale také vnitřní fungování TeXu a práci s boxy a makry.

Můj mladší syn Radek mě požádal, zda bych mu nepomohl vytvořit karetní hru Set. Dokázal by to sice udělat například v Inkscape, ale vzhledem k tomu, že kartičky opakují motivy podle přesně stanoveného pravidla, dospěl správně k závěru, že než by vytvořil všech 81 kartiček, že by se uklikal a uklonoval k uzoufání. Chtělo by to tedy nějaký programovací jazyk a kartičky naprogramovat. Původně ho napadlo, že když umím ten PostScript, že to napíšu v PostScriptu. Šlo by to, ale rozhodl jsem se pro TeX.

Obsah

• Popis kartiček
• Cyklus k vytvoření kartiček
• Sestavení jedné kartičky
• Vykreslení jednoho tvaru
• Závěrečný tisk

Popis kartiček

Na každé kartičce se nachází jeden ze tří tvarů:

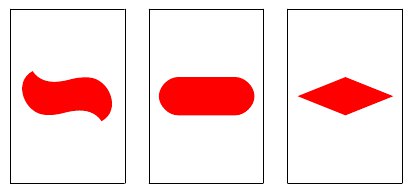
Každý tvar může být plný, šrafovaný nebo prázdný:

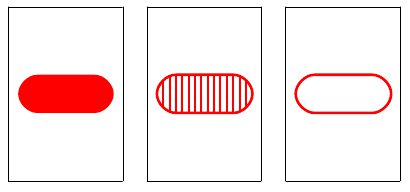
Každý tvar (vždy stejný a se stejnou výplní) se na kartě může objevit jednou, dvakrát nebo třikrát:

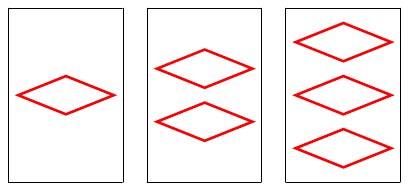
Každá karta je vytvořena v barvě červené, modré nebo zelené:

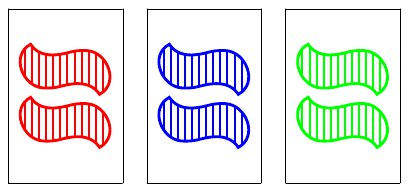
Rozpoznáváme tedy čtyři charakteristiky na každé kartě a každá charakteristika může mít tři stavy. To je tedy dohromady 3⁴ = 81 karet.

Tyto kartičky nyní naprogramujeme v TeXu. Kompletní příklad si můžete stáhnout jako zdrojový soubor pro pdfTeX. Můžete si jej vyzkoušet zpracovat příkazem pdftex karty-set nebo pdfcsplain karty-set. V následujícím textu vyberu vždy některé řádky z ukázky a podrobně vysvětlím jejich smysl.

Cyklus k vytvoření kartiček

Zkusme si z příkladu vytáhnout jen následující řádky:

\def\tvary#1{\if^#1^\else \def\stvary{#1}\barva CZM{}\expandafter\tvary \fi}
\def\barva#1{\if^#1^\else \def\sbarva{#1}\pocet 123{}\expandafter\barva \fi}
\def\pocet#1{\if^#1^\else \def\spocet{#1}\plnost FSE{}\expandafter\pocet \fi}
\def\plnost#1{\if^#1^\else \def\splnost{#1}\udelej \expandafter\plnost \fi}
\def\udelej{\message{\stvary,\sbarva,\spocet,\splnost}}

\tvary BOK{}
\end

Tento kód zavolá postupně 81krát makro \udelej, přitom při každém volání jsou nějak (pokaždé jinak) natavena následující makra:

\stvary ... B (brambora), O (ovál), K (kosočtverec)
\sbarva ... C (červená), Z (zelená), M (modrá)
\spocet ... 1 (jednou), 2 (dvakrát), 3 (třikrát)
\splnost .. F (plně), S (šrafovaně), E (obrys)

Podle hodnot těchto čtyř maker se tedy makro \udelej dozví, jakou má vytvořit kartu. Jak to udělá, si povíme za chvíli. Nyní se zaměříme na pochopení uvedeného čtyřnásobného cyklu. Zaměříme se nejprve na první řádek:

\def\tvary#1{\if^#1^\else \def\stvary{#1}\barva CZM{}\expandafter\tvary \fi}

Zavoláme-li \tvary BOK{}, vezme si makro \tvary nejprve první parametr B (ten je v makru formálně označen #1) a provede:

\if^B^\else \def\stvary{B}\barva CZM{}\expandafter\tvary \fi

Test \if sleduje shodnost prvních dvou tokenů, tj. ^ a B nejsou shodné. Provede se tedy část kódu za \else:

\def\stvary{B}\barva CZM{}\expandafter\tvary \fi

Zde je definováno \stvary jako B a dále se provede \barva CZM{}. Symbol \fi ukončuje text, který se vykonává za \else. Konstrukce \expandafter\tvary\fi nejprve pomocí \expandafter odstraní ukončovací symbol \fi a teprve poté spustí znovu makro \tvary. Makro \tvary tedy volá samo sebe (rekurze). Ve čtecí frontě parametrů nyní už čeká jen OK{}. Makro \tvary tedy provede ještě to samé s písmenem O a s písmenem K. Jakmile je makro \tvary zavoláno počtvrté, přečte prázdný parametr (ten se v TeXu zapisuje jako {}) a expanduje na:

\if^^\else \def\stvary{}\barva CZM{}\expandafter\tvary \fi

Nyní tedy je podmínka \if splněna (znak ^ je roven znaku ^) a makro vykoná to, co je psáno před \else, tedy nic. Tím je cyklus ukončen.

Je dobré si povšimnout, že v každém ze tří volání makra \tvary bylo provedeno \barva CZM{}, takže analogicky se třikrát vyvolá makro \barva. Toto makro v každém volání třikrát volá makro \pocet, to zas třikrát volá makro \plnost a to třikrát zavolá makro \udelej. Máme tedy 81 volání makra \udelej. Makro \udelej zatím v této fázi testování pouze vypíše pomocí \message na terminál a do logu hodnoty maker \stvary, \sbarva, \spocet, \splnost.

Sestavení jedné kartičky

Nyní přesvědčíme makro \udelej, aby vykonalo svou práci:

\def\udelej{\message{\stvary,\sbarva,\spocet,\splnost}%
   \hbox{\vrule \vbox to8.7cm{\hrule\vss 
                              \tmpnum=0
                              \loop \kreslitvar 
                                    \advance\tmpnum by1
                                    \ifnum\tmpnum<\spocet \kern63bp \repeat
                              \vss\hrule}%
         \vrule}\penalty0\kern-.4pt
}

Makro vytvoří \hbox, uvnitř kterého je tenká svislá linka \vrule, dále tam je \vbox vysoký 8,7 cm a konečně znovu svislá linka \vrule. Výška \vboxu určuje výšku kartičky a obsahem tohoto \vboxu (mezi { až }) je nejprve \hrule (nahoře se vytvoří tenká vodorovná linka), pod ní následuje pružná mezera \vss, pak se cyklem \loop vykreslí jeden až tři tvary, pak následuje druhá mezera stejné pružnosti \vss, takže kresba bude vertikálně uprostřed. Nakonec se uvnitř \vboxu vykreslí spodní linka \hrule. Schématicky to vypadá takto:

    /   |       /----hrule----\   |   \
    :   |       :     vss     :   |   :
    :   |       :             :   |   :
hbox: vrule vbox: kreslitvary : vrule : penalty0 kern-.4pt
    :   |       :             :   |   :
    :   |       :     vss     :   |   :
    \   |       \----hrule----/   |   /

Jednotlivé boxy \hbox a \vbox samy nevytvoří kolem sebe mezery ani rámeček, pouze určují, zda sazba v nich má probíhat zleva doprava (\hbox) nebo shora dolů (\vbox). Obrys kartičky je tedy vykreslen natahovacími linkami \vrule a \hrule. Linky \vrule se natáhnou na výšku boxu, ve kterém se nacházejí a linky \hrule se natáhnou na šířku boxu, ve kterém se nacházejí. Šířka našeho \vboxu je určena šířkou sazby, kterou vykreslíme tvary (jak uvidíme za chvíli, je to 5,7 cm). Příkaz \penalty0 za \hboxem dovolí TeXu za kartičkou zlomit řádek a konečně \kern-.4pt je negativní mezera, která je v šířce linky. Takže další karta vpravo, bude-li kladena bez mezery, svou úvodní linkou překryje závěrečnou linku, takže celková linka mezi kartami nezdvojnásobí svou šířku.

V cyklu \loop je nejprve vykreslen požadovaný tvar pomocí makra \kreslitvar. Pak je zvětšeno pomocné \tmpnum o jedničku a je-li menší než požadovaný počet tvarů \spocet, bude se cyklus opakovat. V takovém případě je mezi tvary vložena vertikální mezera \kern63bp, tedy 63 bodů. Nakonec se tedy vykreslí jeden až tři tvary podle hodnoty makra \spocet.

Vykreslení jednoho tvaru

Jeden tvar vykreslí makro \kreslitvar, které je definováno takto:

\def\kreslitvar{\hbox to5.7cm{\kern.5cm\csname tvar\stvary\endcsname\hss}}

Vidíme, že tvar je schován v \hboxu šířky 5,7 cm, což nakonec udává šířku jedné kartičky. Zleva tohoto boxu je nejprve vodorovná mezera 0,5 cm a pak následuje vlastní vykreslení tvaru pomocí:

\csname tvar\stvary\endcsname

Box je po vykreslení tvaru až k pravému okraji vyplněn pružnou mezerou \hss. Výše uvedená konstrukce s \csname...\endcsname expanduje na makro se jménem, které je mezi těmi příkazy napsáno. Protože \stvary je buď B nebo O nebo K, expanze vede na \tvarB nebo \tvarO nebo \tvarK.

Podíváme se, jak je definováno třeba makro \tvarK:

\def\tvarK{\pdfliteral{q
                       \csname barva\sbarva\endcsname
                       .9 0 0 .9 0 0 cm   % transformační matice
                       4 w   % šířka čáry 
                       0 0 m 75 30 l 150 0 l 75 -30 l h   % kosoštverec
                       \uzavritvar 
                       Q
}}

Toto makro udělá kresbu pomocí PDF kódu vymezeného příkazem \pdfliteral. Nejprve je zahájena lokální skupina v PDF kódu příkazem q. Dále se spustí nastavení barvy dvojicí \csname...\endcsname, tedy expanduje se \barvaC nebo \barvaZ nebo \barvaM. Tyto barvy jsou definovány jako odpovídající PDF kód na změnu barvy:

\def\barvaC{1 0 0 RG 1 0 0 rg }
\def\barvaZ{0 1 0 RG 0 1 0 rg }
\def\barvaM{0 0 1 RG 0 0 1 rg }

V makru \tvarK pokračuje PDF kód na vykreslení kosočtverce: .9 0 0 .9 0 0 cm je nastavení velikosti, resp. transformační matice, 0 0 m 75 30 l 150 0 l 75 -30 l h je příprava obrysu kosočtverce. Obrys je uzavřen makrem \uzavritvar a nakonec je ukončena lokální skupina v PDF kódu příkazem Q.

Makro \uzavritvar řeší, zda připravený obrys obtáhne čarou, vyplní nebo vyšrafuje:

\def\uzavritvar{%
   \if S\splnost W S 3.5 w \srafa||||||||||||||{}
   \else \if F\splnost f
         \else S \fi
   \fi
}

Je-li \splnost nastavena na S (šrafy), vloží se do PDF kódu příkazy W S, které vykreslí připravenou křivku a použijí ji jako ořezovou. Dále je makrem \srafa nakresleno šrafování. Je-li naopak \splnost nastavena na F (plný tvar), vykreslí se křivka PDF příkazem f, tj. výplň. V posledním případě se křivka vykreslí příkazem S, tedy obrys.

Makro \srafa samotné je definováno takto:

\def\srafa#1{\if^#1^\else 1 0 0 1 10 0 cm 0 -30 m 0 80 l S \expandafter\srafa\fi}

Tuto smyčku s rekurzivním voláním sebe sama už známe. Makro \srafa je voláno tolikrát, kolik je za ním svislých čar. Opakovaně tedy klade do argumentu \pdfliteral PDF kód ve tvaru:

1 0 0 1 10 0 cm 0 -30 m 0 80 l S

Tento kód posune aktuální kresbu pomocí transformační matice o 10 bodů doprava a následně vykreslí čáru z bodu (0, −30) do bodu (0, 80).

Ostatní tvary \tvarO (ovál) a \tvarB (brambora) jsou udělány obdobně. Můžete se na ně podívat do  zdrojového kódu celého příkladu.

Dodám ještě, že souřadnice kosočtverce a oválu jsem napsal „z voleje“ přímo v textovém editoru. V případě té brambory by to šlo taky, ale rychlejší bylo vykreslit si bramboru v Inkscape, uložit výsledek jako EPS a z tohoto EPS vytáhnout odpovídající PDF kód. Proto tam vidíte desetinná čísla. Nedošlo by asi k příliš velkému zkreslení, kdyby byla tato čísla zaokrouhlena na čísla celá.

Závěrečný tisk

Pomocí \noindent zahájíme odstavec bez odstavcové zarážky, pak se pomocí \tvary BOK{} vytiskne 81 kartiček, jakoby to byla písmena v odstavci. Tento odstavec pak TeX zalomí do řádků (vejdou se mu tři kartičky na řádek) a do stránek (vejdou se mu tři řádky na stránku). Vytvoří tedy 9 stránek, které lze pak rozstříhat a získat požadované kartičky. Aby nebyla zdvojena šířka vodorovných linek mezi kartičkami, je nastaveno \lineskip=-.4pt, tedy mezera mezi řádky je záporná v šířce linky. Dále je nastaveno

\rightskip=0pt plus1fil

Příkaz způsobí, že do každého řádku je zprava vložena pružná mezera, bez které by TeX měl potíže s vyrovnáním řádku a dal by to najevo varovnými hlášeními.

       

Komentáře

[AnalProbe]

pohonil jsem

[Milan Vančura]

Krása na počtení k čaji. Když to někdo umí a dá si s tím tu práci, aby odladil veškeré detaily, je to paráda. Aspoň pro mě jsou to vzpomínky na univerzitní časy, kdy jsem tiskl a vázal TeXbook naruby a miloval jsem podobné hříčky. Dnes musím přiznat, že bych to měl několikanásobně rychleji naklonované v inkscape a pokud bych to měl (polo)automatizovat, např. v předtuše dalších úprav, tak bych to rozhodně nedělal v jazyce, kde se cykly píší jako rekurze a kde se do vykonávání kódu plete expanze textu a musím hlídat kategorie znaků (naštěstí tady nebylo explicitně třeba). I kdybych měl napsat párřádkový skript v pythonu, který mi vygeneruje TeXový zdroják už jen s makry \udelej.

Takhle mi to připomíná spíš úlohu do šifrovačky. Zajímavost: za celých několik let běhu soutěže Podrátě jsem nevymyslel dostatečně jednoduchou úlohu v TeXu, aby byla zajímavá. Cokoli zajímavého vyžaduje ladění tolika detailů na tolika úrovních, že by to hráče odradilo. To už bylo snazší vyrobit úlohu ve vimu (úloha 11) - podobný styl "programování" a hezčí "aha" efekt.

[Josef Kufner]

I kdybych měl napsat párřádkový skript v pythonu, který mi vygeneruje TeXový zdroják už jen s makry \udelej.

Přesně tak bych to řešil. (Tedy místo Pythonu bych šáhl po PHP, ale to je jen detail.)

[xkucf03]

To já radši v BASHi nebo Perlu – PHP bych musel na většinu strojů doinstalovat, což se mi nechce – navíc v tom Perlu by se to i psalo líp.

[Bedňa]

To sa hovorí o Perly že zdroják vyzerá rovnako ako binárka, ale tento zápis v Tex ma zabil

[Filip Jirsák]

To je zklamání. Doufal jsem, že bys mne podpořil s XSLT a SVG+FO.

[xkucf03]

To záleží na situaci. Když to bude nějaká jednorázovka, kde člověk pustí dva vnořené cykly a pak si ručně zkontroluje výsledek, tak klidně ten Perl. Jindy radši to XSLT/XQuery/… Taky záleží na okolí: z Javy radši budu volat XSLT než perlovský skript.

[Jindřich Makovička]

V LuaTeXu by se to možná dalo napsat i tak, aby to náhodný kolemjdoucí pochopil :)

[bubla]

Ajajaj, od toho tu přece máme Metapost, Asymptote a bůhvícoještě...

[knedlik]

zbytocnost. myslim ze ten serial o TeXu sa mal uberat inym smerom.

[n]

+1

[olsak]

Ajajaj, od toho tu přece máme Metapost, Asymptote a bůhvícoještě...

Možná by to chtělo ukázat, jak se stejná úloha vyřeší v Metapostu, Asymptote, pythonu a bůhvičemještě, abychom měli srovnání. Jsem přesvědčen, že TeX v tom srovnání vyjde velmi dobře. V cca padesáti řádcích kódu je vše: popisy kreseb, algoritmus pro vygenerování kartiček i jejich konečné vložení do stránek PDF dokumentu.

zbytocnost.

Chápu, že asi k ničemu nevyužijete zrovna tuto karetní hru. V příkladu jsem ale chtěl hlavně ilustrovat, jak TeX vnitřně funguje na nejrůznějších úrovních (makra, boxy, grafika) bez sáhodlouhých popisů jednotlivých algoritmů. Ty si zájemce najde v odpovídající literatuře, např. v TeXbooku naruby.

myslim ze ten serial o TeXu sa mal uberat inym smerom.

Není řečeno, jakým směrem by si čtenář představoval, že by se to mělo ubírat. Až to někdo vyloží, mohu na to reagovat, zda jsem ochoten to takovým směrem psát.

[Katar]

Autore, položte si otázky:

Píšu to za peníze, které mi za to čtenář nebo ABCL dává? Pokud ano, je názor "zbytocnost" k zamyšlení.

Píšu to zdarma, pro širokou veřejnost a s vidinou, že by to mohlo někomu jinémo pomoct? Pokud ano, potom je názor "zbytocnost" je tlacháním někoho, kdo sám umí hovno a potřeboval jen vylít dačo z mozgu, kde už toho privela nebolo...

[knedlik]

samozrejme ze viem o TeXu hovno, preto som sa chcel nieco naucit. resp. som v tom napisal len diplomovku a par clankov do publikacii.

a pisat to pre siroku verejnost ? ty si odkial padol ? ved prva cast bola otvorena 7341, druha 4902 a predposledna 2614. ak toto nie je signal zleho smerovania tak potom neviem co viac treba.

este jedna vec, ked chce clovek ppuzit nejaky priklad tak to ma byt co naviac k realenmu pouzitiu a nie pisat priklad o tvorbe "hry" v TeXu.

[egg]

Až to někdo vyloží, mohu na to reagovat, zda jsem ochoten to takovým směrem psát.

Možná právě to srovnání s jinými řešeními by bylo zajímavé. Mně to skriptování v TeXu pořád připadá trochu moc hardcore a nejsem si jist, proč bych to měl dělat takhle. Já bych zvolil asymptote, protože procedurální/objektový přístup je mému myšlení blíž. (Ovšem každý přednostně použije to, co lépe ovládá.)

[knedlik]

mna by zaujimalo ako urobit knihu > The Velvet Underground: An Illustrated History of a Walk on the Wild Side v TeXu, ci sa to vobec da. ukazka sa da najst na amazone.

[Někdo jiný]

Přílohy:

• karticky.hs (1094 bytů)
• soubor.svg (177417 bytů)

Pojďme srovnávat. V příloze je program v Haskellu, který vygeneruje prakticky totéž, pouze místo PDF použije SVG. Otázka je, nakolik je fér srovnání čistého TeXu a knihovny Diagrams.

[Josef Kufner]

Nebylo by lepší místo rámečků rozmístit karty bez okrajů na papír tak, aby se pak list nařezal podle pravítka na stejné díly?

Jak se vlastně řeší přesné pozicování vůči listu papíru? Když jsem se trefoval na předřezané samolepicí etikety, nebylo to vůbec snadné.

[olsak]

Jak se vlastně řeší přesné pozicování vůči listu papíru?

Je potřeba nastavit \hoffset=-1in a \voffset=-1in. Například:

\hoffset=-1in \voffset=-1in \topskip=0pt \vsize=300mm \nopagenumbers
\newcount\n  \newcount\N

\def\meritko#1#2 {#1{\C
    \loop \advance\n by1 \advance\N by1
          \ifnum\n<#2 \kern1mm
                      \ifnum\N=10 \N=0 \C \else \c \fi
                      \repeat}}

\def\c{\vrule height3mm depth0pt \kern-.4pt }
\def\C{\vrule height3mm depth2mm \kern-.4pt }

\meritko\hbox 211

\def\c{\hrule width3mm \kern-.4pt }
\def\C{\hrule width5mm \kern-.4pt }
\kern5mm \nointerlineskip

\meritko\vbox 288

\end

vytvoří na stránce A4 milimetrové měřítko přesně u horního a levého kraje stránky. TeX ručí přesností na úrovni nanometrů, ale jak se s tím poradí tiskárna, která typicky ne zcela přesně vezme papír, to už je jiná otázka.

[Pavel Čejka]

Btw... nejenže tiskárna vezme papír pokaždé jinak, ale on i výsledek není přesný. Dost tiskáren se liší v nepřesnosti vertikálně versus horizontálně. Narazil jsem na to při tisku předloh pro plošné spoje. Občas jsem musel otočit o 90°, aby nepřesnost byla tolerovatelná. A to dělám malé desky max do 100x100mm, na celou A4 se to projeví 2.97x větší chybou U laserů bývá samozřejmě nepřesnější posuv oproti kresbě laserem na válec.

[Pavel Čejka]

Čistě praktická poznámka nemající s TeXem moc společného - většina tiskáren vezme papír ze zásobníku pokaždé trochu jinak, v lepším případě +- 1mm, často hůř. Málokterá tiskárna umí papír urovnat po podání (a některé to dělají jen při tisku "foto" kvalitou), málokterá tiskárna má víc než jen čidla přítomnosti papíru, kterými pozná, že se nezasekl, ale nepozná, jestli je mírně šikmo, nebo maličko posunutý (a posunutý kolmo k posuvu už vůbec ne). Tím pádem jakékoli ořezávání (řezačkou) jinak, než ručně podle ořezových značek nepřichází v malých objemech tisku v úvahu.

Párkrát jsem zkoušel např. oboustranný tisk tak, aby rub a líc přesně pasovaly. Nejde to. A je docela jedno jestli na laserech, inkoustech, levných srágorách, nebo dražších velkých "kopírkách" (tak kolem 100kKč). Jsou mezi nimi rozdíly, některé to zvládají lépe, ale dokonale žádná. Totéž samolepky, třeba ty na CD, obrázek prostě musel kousek přesahovat, aby posunutí listu nevadilo ... možná snad některá z "opravdu bezokrajových" tiskáren? (což mi připomíná, že jsem neprověřil Epson R2880)

[olsak]

bych to měl několikanásobně rychleji naklonované v inkscape

Já bych to měl několikanásobně rychleji napsané v TeXu.

Možná právě to srovnání s jinými řešeními by bylo zajímavé.

OK, kdo to udělá? Já kvůli tomu nebudu studovat Asymptote ani Metapost, python a další zde zmíněné nástroje. Očekávám, že zde udělá srovnání nějaký uživatel těchto nástrojů.

Takhle mi to připomíná spíš úlohu do šifrovačky

K úloze do šifrovačky se spíše blíží třeba toto. Soubor je třeba zpracovat TeXem (ne LaTeXem). Zkuste si tipnout, co z toho vyleze.

Autore, položte si otázky

Já si ty otázky pokládat nemusím, ovšem nevím, jak to vnímají ostatní. Takže: píšu to pro veřejnost s vidinou, že by to mohlo někomu jinému pomoct, jako ostatně vše, co dělám v souvislosti s TeXem. Mám k tomu domluven velmi drobný honorář, kvůli kterému to rozhodně nedělám.

ved prva cast bola otvorena 7341, druha 4902 a predposledna 2614

To taky sleduji. Navrhnul jsem tedy asi před měsícem šéfredaktorovi, že seriál ukončím, třebaže mám témata na asi dalších pět dílů. Dostal jsem odpověď, že úbytek přístupů je u odborně zaměřeného seriálu obvyklý a že bych mohl pokračovat. Pokud mě ovšem přesvědčíte o opaku vy, čtenáři, samozřejmě pokračovat nebudu. První, co bych potřeboval, je zjistit, co vlastně od seriálu očekáváte. Když napíšete jen slovo ,,zbytečnost`` pak to není příliš konstruktivní.

mna by zaujimalo ako urobit knihu The Velvet Underground ...

Kniha, ve které každá dvojstrana je plná obrázků a jejich usazení je řešeno výtvarníkem individuálně, není vhodný příklad na použití TeXu. Obrázky jsou výtvarníkem usazovány interaktivně na každé dvoustraně dle potřeby a text tvoří jen podružnou část. Těžko můžete usazování obrázků ,,dle pocitu`` dělat tak, že vložíte jejich souřadnice do programu a program vám pak obrázky usadí. Pokud ale je v knize nějaký očekávatelný řád, pak se ten řád naprogramovat dá a vyplatí se to. Tento typ publikace bych dělal zhruba tak, jak popisuji na stranách 275 až 280 TeXbooku naruby.

Příklady, na co se TeX naopak hodí, jsou třeba tady.

Soukromé shrnutí:

V okamžiku, kdy jsem zde poprvé na jednom poměrně jednoduchém příkladě naznačil, jak se v TeXu zhruba programuje, se zde sešly příspěvky o tom, že tento styl programování je neakceptovatelný, že to je hardcore nebo šifrovačka. Je to pro mě poučení, že dnešní programátoři nejsou schopni nebo ochotni takto uvažovat a že bych tedy s tím TeXem měl zde asi přestat obtěžovat. Je to škoda. Možná tím obě strany přicházejí o hodně.

[Tramtarara]

Ne, neprestavejte prosim. Je mnoho uzivatelu kteri radi vase serialy ctou vcetne mne a nijak to nekomentuji. Myslete take na ty, kteri v budoucnu budou hledat pres vyhledavace reseni ktere jim mozna tento Vas cyklus prakticky ukaze.

Brouky Pytliky-Teoretiky, kteri by vsechno udelali lip a rychleji ale jedine co po nich je je vyblitek v kazde diskuzi na kazde tema, ty nechte at si vyzerou svych 5 minut slavy. A hlavne pokracujte. Diky a drzim palce.

[Atrament]

Rozhodně v seriálu pokračujte a nenechte se odradit. Mně osobně jeho směřování velmi příjemně překvapilo, u prvního dílu jsem očekával další seriál na téma 'Začínáme s TeXem', kterých je na netu už kupa, jsem rád že jsem se mýlil, a každý díl si vždy moc rád přečtu.

[Radek]

Také se přimlouvám za pokračování. Jsem sice jen uživatel a asi nikdy nebudu v TeXu nic programovat, ale přesto narážím na hlubší neznalosti, které mě nutí „bastlit“. Seriál mi každopádně pomáhá znalosti doplňovat, takže díky!

Největší radost jsem měl z dílu 8, kde jsem se konečně dozvěděl, jak funguje „magie“ při hledání balíčků. Kromě toho se mi líbily především díly 4, 5 a 7, protože pokrývají problémy, které jsem během používání TeXu potkal.

[juraj-bit]

Tiež sledujem pravidelne tento seriál napriek tomu, že som laik a len občasne požívam LaTeX, aj to len ako nástroj ku svojmu koníčku. Vaše články sú nabité informáciami a preto by bola škoda, ak by ste sa rozhodli to tu utnúť.

Uvítal by som ale nejaký ucelený motív, ktorý by sa rozvíjal naprieč celým seriálom. Teda niečo ako vytvorenie knihy, mierne sa obtrieť o typografiu, jej postupné šperkovanie až po následné konverzie do ebook a iných formátov. Prípadne rozviesť, čo by sa s tým dalo ešte robiť. Možno uviesť aj vhodný softvér na vytvorenie, správu a katalogizáciu vytvorených súborov.

[ebik]

Sice to není dobrý příklad jak naprogramovat vykreslení těchto kartiček, protože je výsledný program pro většinu lidí hůře čitelný (což je dáno syntaxí TeXu), ale je to dobrý příklad na to ja v TeXu programovat. A určitě se někomu stane, že bude řešit úlohu jak implementovat něco podobného jako (parametrické) makro. Volat něco z TeXu a vkládat pak výstup, či volat TeX několikrát (jak to dělá například bibtex), aby se na správná místa doplnily ty správné údaje, může být často složitější, než to samé napsat přímo v TeXu. Takže určitě pokračujte.

[Václav "Darm" Novák]

Tohle je klasika, stížnosti jsou vidět nejvíc Rozhodně bych byl rád za pokračování, i když se příznám, že jsem vaše články zatím jen zběžně proletěl. Pořádně si je přečtu až bude čas

[Bedňa]

+1

[nasson]

Tak já osobně jsem za OPmac velmi vděčný, děkuji. Poslední díly mě také příliš nezaujaly, ale beru to tak, že až si budu chtít pohrát s písmem, tak vím, kde hledat... Bohužel nejsem programátor a do TeXu neproniknu nikdy. Takže např. teď bojuji s literaturou. Citace v OPmac sice řeší proměnu v interval [1-6], ale bohužel se neřeší nutnost seřazení [7,1,3,2]. Zkoušel jsem využít balíček librarian a Sorting in Blue od Kees van der Laan. Ale nepřišel jsem na to, jak to udělat. A přitom automatické seřazení citací je naprostý základ, bez kterého se citace ani nedají používat.

PS. Při použití \verbinput(-) z OPmac se zobrazí nakonec jeden prázdný řádek. Už jsem si makro opravil, ale kdyby se snad OPmac dále updatoval, bylo by pěkné, kdyby bylo možné toto chování změnit.

[Josef Kufner]

Použij LyX a tyto drobnosti nemusíš řešit.

[nasson]

Přiznám se, že jsem LyX nikdy nezkoušel. Ale že by mohl takhle zázračně vyřešit všechny problémy co jsem kdy měl s LaTeXem/TeXem se mi ani nechce věřit.

[olsak]

Citace v OPmac sice řeší proměnu v interval [1-6], ale bohužel se neřeší nutnost seřazení [7,1,3,2].

Děkuji za upozornění na chybu. Opravím to v únorové verzi.

Při použití \verbinput(-) z OPmac se zobrazí nakonec jeden prázdný řádek.

Toto už někdo reportoval, takže v lednové verzi to je opraveno.

Omlouvám se ostatním, toto jistě není prostor pro reportování chyb v OPmac. Kdybych věděl, kdo to je nasson, odpověděl bych mu přímo a nezatěžoval bych tuto diskusi.

[TyPo]

Také bych byl vděčný za pokračování seriálu. Co od seriálu čekám? K TeXu jsem se dostal už dávno při potřebě sazby matematických textů. Matematické texty už moc sázet nepotřebuji, ale potřeba občas něco kvalitně vysázet je. Často jde o něco automaticky generovaného nebo netypického. Návody na užívání LaTeXu jsou všude a není problém v tom něco udělat. Problém ale nastane v případě, kdy potřebuji něco "extra".

Od seriálu očekávám nějaký základ principů TeXu, základní filozofie, na které je TeX postaven. Hodí se i informace, proč je to tam nejspíše uděláno a není to jinak, pokud se nabízí nějaký intuitivnější způsob. Pak to člověku začne do sebe zapadat a dávat smysl.

Tedy ne kuchařku, jak něco udělat. Ani podrobnou referenční příručku. Ale nějaké základy principů, které člověk musí pochopit. Zbytek už se někde najde.

[ghibulo]

Také se přidávám k tomu, abyste pokračoval, těším se na každý další článek, protože dost informací zde prezentovaných se těžko někde jinde dolují. Hlavně mě zajímají témata, která by mi pomohla jakýmkoliv způsobem dosáhnout u TeXu i jiných výstupů než pdf/ps ... ten díl s html se mi dost líbil.

[olsak]

Děkuji všem, kteří vyjádřili zájem o seriál. Těší mě to. Zvažuji ještě následující témata:

• Koncept box-penalty-glue a další principy sestavování sazby
• Spolupráce s externími programy
• Matematická sazba
• Mikrotypografie

Příklad v tomto díle seriálu měl mimo jiné ukázat způsob uvažování při práci s makry. Tomuto druhu uvažování se nevyhnete, když budete chtít číst cizí makra i tvořit vlastní. Možná to někoho zaskočilo, protože příklad kombinuje makra s PDF kódem na nízké úrovni, ale i to byl záměr: ukázat, že TeXová makra dokáží spolupracovat s grafikou.

Vzhledem k tomu, že mnoho programátorů skutečně není ochotno takto uvažovat, vznikl asi LuaTeX, který umožňuje kombinovat makrojazyk s jazykem Lua. Otázka je, zda to je ideální, zda by se spíš neujal zcela nový procedurální či objektový jazyk prorostlý s algoritmy sazby. Ale o ničem takovém zatím nevím.

[Radek]

Přimlouvám se hlavně za první téma. Druhé mě také zajímá, i když je okrajovější. U zbývajících dvou by záleželo, jak konkrétně se uchopí...

[TyPo]

Děkuji, že zvažujete další díly, a samozřejmě i za ty hotové. Témata 2, 1 a 3 mi přijdou podle názvu zajímavé (asi v tomto pořadí, ale nejvíce bude záležet na konkrétním obsahu). U matematické sazby mě moc nenapadá, o čem by to bylo. Pokud by to byla kuchařka, jak něco vysázet, napsat symbol, zlomek, integrál, matici, ... tak mi to moc zajímavé nepřijde. Pokud by šlo o nějaké principy, mohlo by to být pro mě zajímavé, i když matematických dokumentů už moc nesázím.

Jinak způsob programování v TeXu mi přijde asi jako řadě ostatních mírně řečeno zvláštní. Tedy není to na první pohled moc čitelné a nevidím v tom nějaké výhody oproti konvenčnímu (zejména procedurálnímu) programování. Nicméně dá se na to zřejmě zvyknout. U tvorby grafiky typu tyto karty lze použít spoustu nástrojů, protože tam není třeba řešit sazbu textů. Nakonec by to myslím šlo celkem dobře napsat např. přímo v Postscriptu. Ovšem tam, kde je třeba řešit kvalitní sazbu textů, moc alternativ k TeXu (a jeho nadstavbám a variacím) nevidím. V dnešní době by šel jistě navrhnout a implementovat nástroj, který by řešil sazbu kvalitně jako TeX, ale byl intuitivnější pro programování. Ale není to rozhodně tak snadný úkol, jak se může na první pohled zdát a podle toho vypadá (ne)existence dalších podobných nástrojů.

Nejsem TeX purista, abych všechno implementoval za každou cenu v TeXu. Tedy pokud např. lze vygenerovat snadno zdroják TeXu něčím jiným a vyhnout se tak nehezkému programování v TeXu, rád tak učiním. Jenže ono to vždy nelze, protože ten generátor nemá zpětnou vazbu o rozměrech jednotlivých částí dokumentu apod.

Takže naučit se programovat v TeXu vidím (pro sebe) jako nutnost. A tento díl seriálu se mi líbil. Ne, že bych takto někdy potřeboval sázet karty (to zvládnu i bez TeXu), ale pěkně jsou na tom vidět některé věci v programování TeXu, které jsem neznal. A i to použití vkládání částí PDF zde bylo pěkně ukázané.

Mimochodem víte někdo o nějakém rozumném zdroji informací o PDF mimo oficiální specifikaci? Možná neumím hledat, ale ono se to těžko hledá, protože slovo PDF se vyskytuje skoro všude. Občas jsem narazil na nějaký kratší článeček (http://www.mactech.com/articles/mactech/Vol.15/15.09/PDFIntro/index.html apod.), ale nic trochu většího rozsahu. Specifikace není vyloženě nečitelná, ale třeba existuje něco lepšího, o čem nevím.

[Bedňa]

Co by ma zujimalo, sadzba, typografia, ako to vidi autor a porovnanie z moznostami na dnesnom webe a editoroch. Preco byva kerning spravidla spraseny? Pardon za diakritiku, ale pisem to z kompu kde instalujem Linux.

[Josef Kufner]

Jedna z věcí, které není věnováno příliš pozornosti, je generování PDF dokumentů z různých aplikací – všelijaké reporty, faktury, tiskové verze čehokoliv. Jak zajistit elegantní napojení na zdroj dat? Jak může TeX spolupracovat s šablonovacími systémy? Jak připravit šablony tak, aby se nerozpadly při trochu delším textu? Co když mi tam napíše někdo své jméno azbukou? Co když má někdo ve jméně ošklivé znaky? … Oh. Yes. Little Bobby Tables, we call him.

[Tomáš Pecina]

Autorovi patří můj velký dík: nebýt jeho, o TeXu bych asi pořád jen "pasivně věděl". Takto jsem ho začal využívat a píšu v něm i několik dokumentů denně.

Faktem tedy je, že texová makra připomínají konstrukce Brainfucku a napsat něco s \expandafter je založeno na obdobných principech jako hanojská věž, ale proč bychom se tím měli trápit, když to prostě funguje?

[Radek]

:) Při čtení popisu makra \expandafter mi běhal mráz po zádech. Úplně existenciální zážitek to byl...

[olsak]

Příkaz \expandafter je tradičně zlomový při poznávání TeXu. Kdo jej pochopí, smíří se i s výskytem několika \expandafter za sebou a začne číst makra a tvořit vlastní, přechází z role pasivního uživatele TeXu do role aktivního uživatele, který dokáže TeX krotit podle vlastních představ, nikoli podle toho, co pro něj naprogramoval někdo jiný. Ne nadarmo je v TeXbooku naruby příkazu \expandafter věnována celá sekce 2.2.

Kdysi jsem někde slyšel nebo četl, že Knuth cca po dvaceti letech po zrození TeXu v nějakém rozhovoru prohlásil, že kdyby to měl dělat znovu, udělal by to víceméně stejně. O myšlence zahodit expandovaný makrojazyk a nahradit jej jazykem procedurálním či dokonce objektovým tam nepadlo ani slovo. Soukromě se domnívám, že to souvisí s jedním Knuthův omylem: že všichni uživatelé, kteří budou jeho programy používat, budou dosahovat aspoň zdánlivě srovnatelné inteligence, jakou má on. Kdyby tu nebyl tento omyl, měli bychom uživatelsky přístupnější jazyk spřažený s algoritmy sazby, možná by to i přerostlo ve všeobecně přijímaný standard na zpracování dokumentů.

Zmíněný omyl se názorně promítl na Metafontu, který umělo použít jen pár lidí na světě, co by na prstech rukou člověk spočítal. Fonty se v tom tedy moc nedělaly a dnes Metafont nepoužije skoro nikdo. A TeX je něco podobného. Přežil jen díky Lamportovým ne zcela povedeným makrům (LaTeX) a díky Spivakovým makrům, která přijala Americká matematická společnost jako svůj de facto standard (AMSTeX).

Myslím si, že TeX tu bude dále, budou-li existovat lidi, kteří jej umějí aktivně používat. Proto se snažím lidem nabízet nejen hotová řešení, ale hlavně komentáře a návody, jak je to uděláno. Například dokumentace k OPmac může sloužit taky jako učebnice makroprogramování. Zahrnuje vlastnosti srovnatelné s celým LaTeXem včetně mnoha jeho balíčků.