DSP kuchařka: změna frekvence, filtrace, podvzorkování

15.8.2021 02:36 | Přečteno: 3765× | Meteopress | | poslední úprava: 15.8.2021 02:36

V druhém díle DSP kuchařky se podíváme na posunutí signálu na jinou frekvenci a filtrování lowpass/bandpass filtrem.

Rotátor a jeho numerický výpočet

V předchozím příspěvku jsme viděli, že vzorečkem e^{-i*postupně_se_zvětšující_číslo} vytvoříme bod rotující po jednotkové kružnici v komplexní rovině, čili signál na nějaké frekvenci. Počítat to ovšem z definice, tj. funkcí exp, není moc dobré:

• Je to pomalé - vyhodnocení exp vyžaduje použití netriviálních floatových operací.
• Není to přesné - argument se neustále zvyšuje, a pro dlouhé sekvence bude tak velký, že dojde ke ztrátě přesnosti ve floatovém počítání.

Jenom pro představu v jakých délkách sekvence se pohybujeme, tak pokud samplujete 10 MS/s (standardní hodnota u trošku lepších rádií) a běží to celý den, tak potřebujete bilion vzorků.

Vyřešíme to tím, že zvoleným bodem budeme rotovat pomocí matice rotace, kterou si na začátku předpočítáme a pak už na ni nesáhneme. Případ pro matici 2x2 je na Wikipedii přímo rozepsán a vyžaduje 4 floatová násobení, 1 sčítání a 1 odčítání.

Problém s opakovaným násobením nějakou maticí, přičemž výsledek má být vždycky jednotkový vektor (a mění se jenom jeho směr), je, že se vlivem nepřesností může tento vektor časem prodlužovat nebo zkracovat - spočítaná matice rotace může mít vlivem nepřesností třeba normu 0.99999 nebo 1.00001, takže vektor s každou iterací nepatrně natáhne nebo smrskne, a po výše zmíněném bilionu vzorků to naprosto ustřelí. Proto je potřeba vektor rotátoru občas normalizovat, tj. spočítat jeho skutečnou velikost a tou ho vydělit, čímž se z něj zase stane vektor jednotkový. V praxi se normalizuje každých 512 nebo 1024 vzorků.

Ukážeme si výrobu rotároru pro frekvenci 0.95 radiánů na vzorek (tu jsem si vycucal z prstu a nechtěl jsem aby to bylo přesně 1, protože se třeba může zjistit, že sin(1) mají knihovny předpočítaný). Kód úmyslně nepoužívá komplexní aritmetiku, aby bylo vidět, co se skutečně počítá. A napsal jsem to v C, protože neumím Python/NumPy přesvědčit, aby počítalo v jednoduché přesnosti (ano, polím se dá nastavit dtype=float32, ale skalární operace se furt dělají v doublech). Nejdříve samotný kód v C:

#include <stdio.h>
#include <complex.h>
#include <math.h>
int main() {
  const int nsamples = 110000;
  const float freq = 0.95;

  // naivní implementace s exp
  FILE * ef = fopen("/fs/ef.cfile", "wb");
  for(int i = 0; i<nsamples; i++) {
    complex float result = cexpf(I * freq * i);
    fwrite_unlocked(&result, 8, 1, ef);
  }
  fclose(ef);


  // implementace s rotací pomocí předpočítaných hodnot
  FILE * mf = fopen("/fs/mf.cfile", "wb");

  float rot_cos = cosf(freq);
  float rot_sin = sinf(freq);

  float re = 1;
  float im = 0;
  for(int i = 0; i<nsamples; i++) {
    fwrite_unlocked(&re, 4, 1, mf);
    fwrite_unlocked(&im, 4, 1, mf);

    float re_new = re * rot_cos - im * rot_sin;
    float im_new = re * rot_sin + im * rot_cos;

    re = re_new;
    im = im_new;

    if(i % 10240 == 0 && i > 0) { // úmyslně hodně, aby bylo vidět, jak to diverguje
      float abs = hypotf(re, im);
      re = re/abs;
      im = im/abs;
    }
  }
  fclose(mf);
}

A vyhodnocení:

#!/usr/bin/env python3

import numpy as np
import matplotlib.pyplot as plt

rotator_from_exp = np.fromfile("/fs/ef.cfile", dtype=np.complex64)
rotator_matmul = np.fromfile("/fs/mf.cfile", dtype=np.complex64)

ax = plt.subplot(211)
plt.title("Rozdíl fáze po sobě jdoucích vzorků")
plt.plot(np.fmod(np.angle(rotator_from_exp[:-1]) - np.angle(rotator_from_exp[1:]) + np.pi, 2*np.pi) - np.pi, label="exp")
plt.plot(np.fmod(np.angle(rotator_matmul[:-1]) - np.angle(rotator_matmul[1:]) + np.pi, 2*np.pi) - np.pi, label="matmul")
plt.legend()

plt.subplot(212, sharex = ax)
plt.title("Absolutní hodnota (měla by být 1)")
plt.plot(np.abs(rotator_from_exp))
plt.plot(np.abs(rotator_matmul))

plt.show()

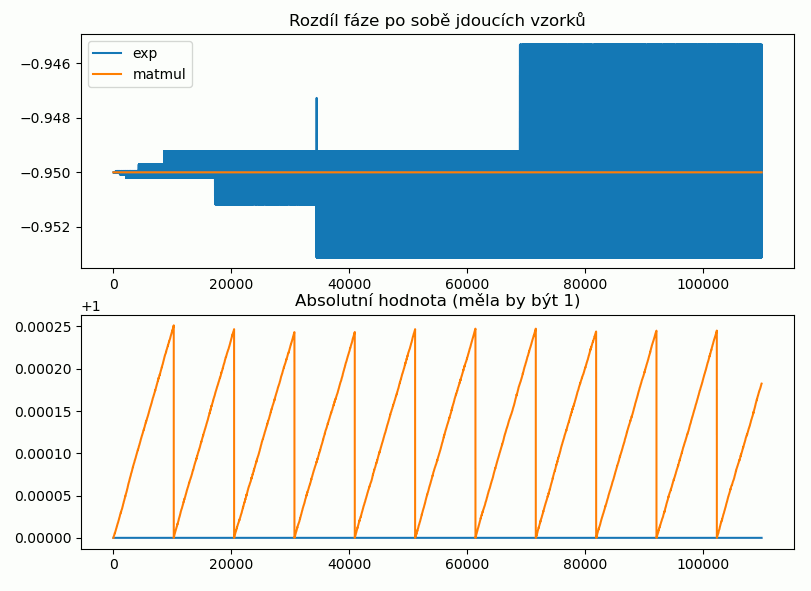
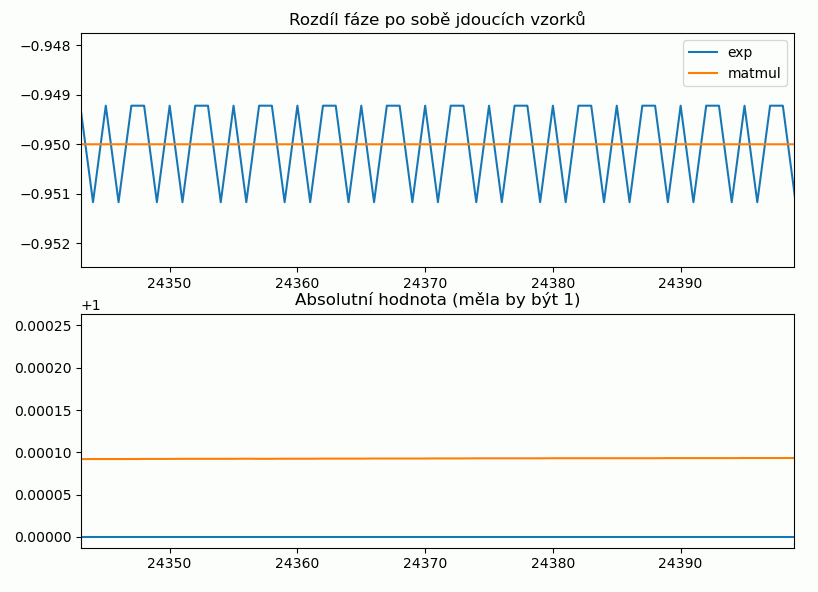
Vidíme, že fáze u naivního počítání začne být velmi brzy nepřesná. Oproti tomu rotátor s použitím matice diverguje v absolutní hodnotě - ale zde je schválně nastavená normalizace málo často, aby to bylo vidět. Zde ještě detail, na kterém je vidět, jak cexpf šumí:

Chirp - vzorový signál

Jako ukázkový signál si vygenerujeme chirp. Jde o signál s postupně rostoucí frekvencí a používá se jako nejjednodušší varianta rozprostřeného spektra. Jak na to? Výše jsme měli e^{-i*lineárně_se_zvětšující_číslo} a byla to konstantní frekvence. Pokud budeme zvětšovat zvětšování toho čísla, bude se zvětšovat i frekvence. Nejjednodušší je i toto zvětšování dělat lineárně, čili to bude e^{-i*kvadraticky_se_zvětšující_číslo}. Proto se tomu taky někdy říká signál s kvadratickou fází. Vyrobíme to takto:

nsamples = 10240
dphase = 15

quadratic_ramp = np.linspace(-dphase, dphase, nsamples)**2

df = quadratic_ramp[0] - quadratic_ramp[1]
hbin = 256 - df * 512
print("Frekvenční výchylka jednostranná: %f Hz; pro FFT velikosti 512 očekáváme %i. bin"%(df, hbin))

chirp = np.exp(2*np.pi*1j*quadratic_ramp)

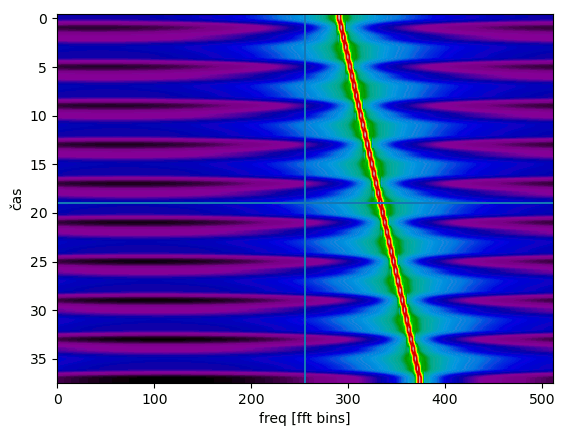
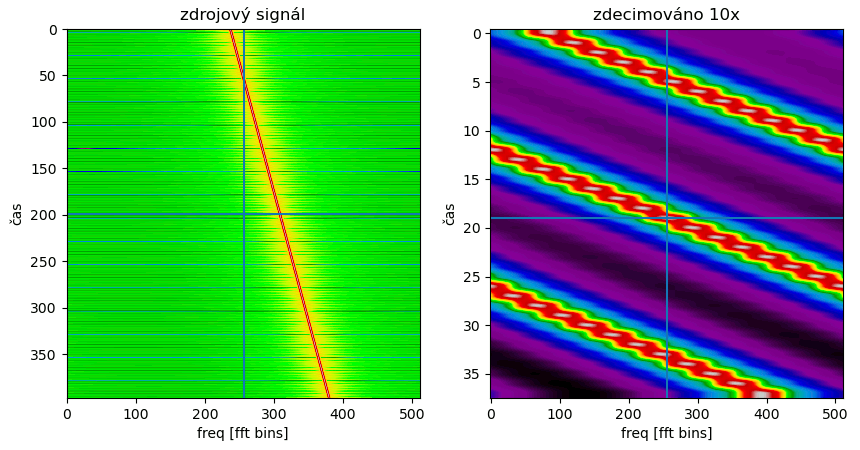
Nakreslíme si waterfall jako minule (vyznačil jsem do něj středové osy a 211. bin, aby šlo porovnat, na jaké frekvenci to začíná a jakou jsme spočítali):

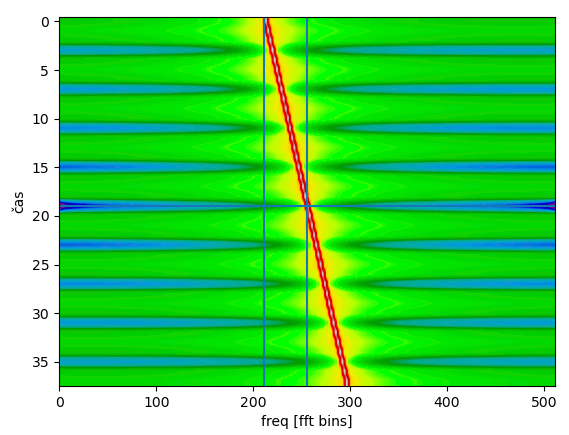
Mimochodem zde by signál měl být dokonale čistý a tedy ty artefakty jsou asi artefakty vzniklé použitím okýnka.

Změna fáze

Fázi signálu posuneme vynásobením e^-i*konstanta. Normálně bych to sem nedával, ale zrovna jsem to nedávno použil (poprvé) - debugoval jsem radar tak, že jsem koukal na odraz od vzdáleného kopce, a porovnával jsem ho s tím, co si myslím, že vysílám. Pokud to souhlasí, tak se tím ověří, že celá ta cesta (od vymyšlení signálu, přes jeho vygenerování, zesílení, odvysílání, putování atmosférou, odraz, přijetí, ofiltrování a analýzu) funguje. Ale signál samozřejmě přijde náhodně fázově posunutý - a aby to šlo porovnat, tak se musí posunout zpátky.

otocenej = chirp * np.exp(-1j*0.95)

Posunutí frekvence

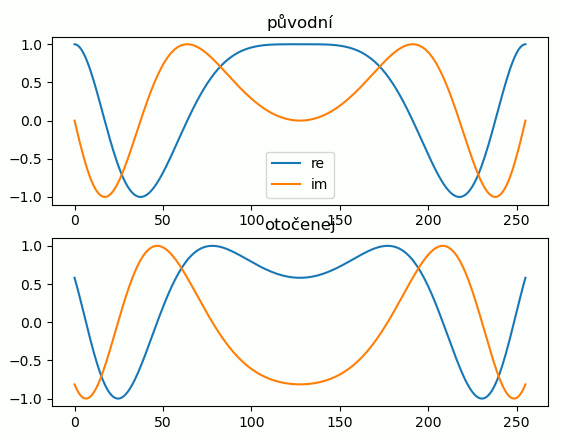
Další běžná operace je posunutí (změna) frekvence signálu. Provede se vynásobením (po složkách) s rotátorem. Já tady použiju adhoc vyrobený z definice, ale jak jsme psali výše, pro delší signály se to musí vygenerovat chytřeji. Takhle ho posuneme ve frekvenci o 0.95 radiánů na sample:

freq=0.95
posunutej = chirp * np.exp(1j*np.linspace(0, nsamples*freq, nsamples))

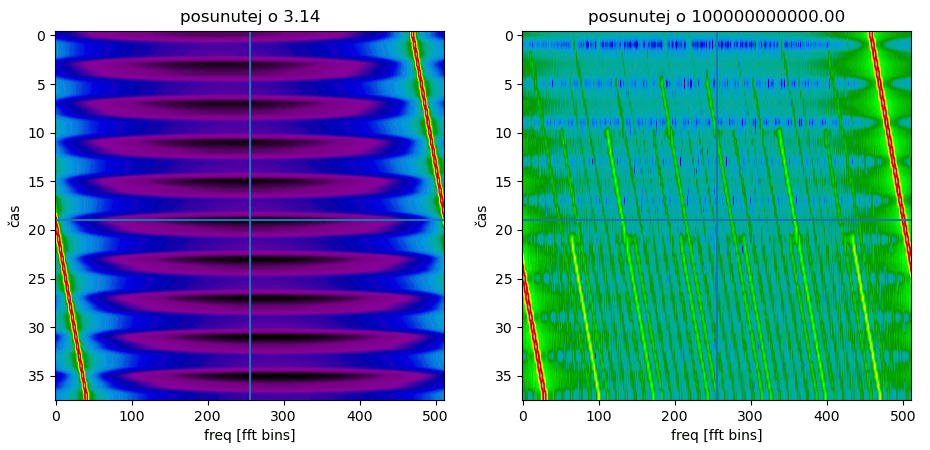
Zkuste si, co se stane, když ho posunete o -1, o PI (wrapne se to), o 1000, o 100000000000 (zaokrouhlovací chyby se projeví i při počítání v doublech).

Pokud chcete tohle dělat s delšími signály, doporučuji použít příslušnou funkci z Volku, jejich implementace je ručně vektorizována pomocí SSE a AVX instrukcí.

Filtrace pomocí lowpass filtru

Často je potřeba vybrat ze signálu oblast (ve frekvencích) od-do a zbytek potlačit. K tomu budeme potřebovat lowpass FIR filtr. To je pole koeficientů, se kterými se signál zkonvolvuje. Vyrobit se dá GNU Radiem, jak jsme řešili v článku o GNU Radiu, ale SciPy na to má taky funkci. První parametr říká délku filtru (čím delší, tím ostřejší bude mít filtr hrany, ale asi bude mít horší nějaké parametry co rozmazávají v čase a bude náročnější na vyhodnocení, zejména pokud se to nebude vyhodnocovat FFT jak je popsáno níže), druhý říká, kolik pásma se má propustit. Někdy je potřeba filtr speciálního tvaru (např. raised cosine), to pak záleží na konkrétní aplikaci.

coeffs = scipy.signal.firwin(64, 0.1)

Zkonvolvujeme ho se signálem:

filtered = np.convolve(chirp, coeffs, "same")

Protože možná není na první pohled vidět, jak funguje konvoluce komplexního a reálného filtru, tak to rozepíšu:

filtered2 = np.convolve(np.real(chirp), coeffs, "same") + 1j * np.convolve(np.imag(chirp), coeffs, "same")
print(np.allclose(filtered, filtered2))  # True

tj. reálnou a imaginární složku natahujeme zcela nezávisle.

Mód konvoluce (zde same) říká, co se má dělat na krajích, kde se signál a filtr plně nepřekrývají. same vrátí stejně dlouhý výstup jako je vstup, tj. jakoby tam vždycky nechá půlku té nevalidní oblasti. Pak ještě existuje valid (vrací kratší výstup, a to pouze data, kde došlo k plnému překryvu) a full (delší výstup, všude kde byl překryv nenulový).

Někdy je potřeba nemít lowpass, ale vybrat si signál, který není na nulové frekvenci / není symetrický podle středu. Naštěstí filtr lze posouvat úplně stejně jako signál, a tak můžeme posunutím z lowpassu udělat bandpass. Takový filtr bude komplexní, filtry, které nejsou symetrické kolem nuly, musí být komplexní.

coeffs_shifted = coeffs * np.exp(1j*np.linspace(0, len(coeffs)*0.95, len(coeffs)))
filtered_shifted = np.convolve(chirp, coeffs_shifted, "same")

Konvoluce pomocí FFT s využitím věty o konvoluci

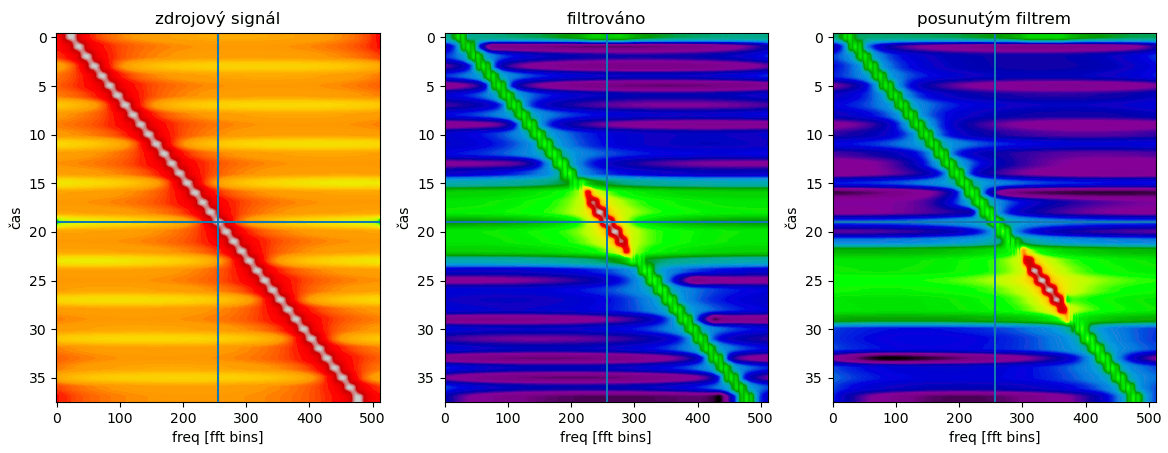
Konvoluce může být poměrně pomalá: v každém bodě výstupního signálu musíte provést tolik násobení, kolik je délka filtru. Pokud je navíc filtr komplexní (bandpass z předchozí kapitoly), tak jsou i tato násobení komplexní. Pro dlouhé filtry, které mohou mít třeba 1500 tapů, je to tak obtížně použitelné. Nyní se dostáváme k tomu, co jsem zmínil v předchozím díle: problém přeformulujeme tak, aby šlo aplikovat FFT, provést nějaký rychlý výpočet, a aplikovat zpětnou FFT. A takové přeformulování konvoluce právě nabízí Věta o konvoluci. Říká, že konvoluci lze provést následujícím algoritmem:

• Zvolíme velikost FFT. Do té se musí vejít signál a filtr a současně by to měla být velikost, pro kterou se FFT snadno počítá, tj. mocnina dvojky. Pokud nás zajímá mód konvoluce full, musí být velikost FFT signál + filtr - 1; pokud nám stačí same nebo valid, stačí filtru půlka (protože to ve skutečnosti počítá cyklickou konvoluci a ty půlky se potkají v místě, které budeme zahazovat, protože není valid) nebo snad pro valid tam žádné místo navíc být nemusí.
• Signál a filtr doplníme nulami na zvolenou velikost FFT.
• Signál a filtr ztransformujeme.
• Ztransformované výsledky vynásobíme po složkách.
• Vynásobený výsledek ztransformujeme zpět.
• Z výsledku vezmeme začátek (odpovídá full), resp. úsek co nás zajímá.

FFT má složitost NlogN a násobení po složkách má složitost N, zatímco konvoluce počítaná přímo ze vstupních dat měla složitost N*M (pro M=délka filtru). Pro dlouhé filtry a husté [ve smyslu dense = opak sparse] výstupy se to tak nejspíš vyplatí. Tady je implementace:

# right-pad numpy array to size with zeros
def padto(a, size):
  return np.pad(a, (0, size - len(a)), mode="constant")

# velikost FFT, kterou budeme používat
fftsize = 16*1024

# FIR doplníme nulami na velikost FFT a ztransformujeme
coeffs_shifted_padded = padto(coeffs_shifted, fftsize)
coeffs_shifted_padded_fft = np.fft.fft(coeffs_shifted_padded)

# signál doplníme nulami na velikost FFT a ztransformujeme
chirp_padded = padto(chirp, fftsize)
chirp_padded_fft = np.fft.fft(chirp_padded)

# vynásobíme po složkách ztransformované
convolved_fft = coeffs_shifted_padded_fft * chirp_padded_fft

# ztransformujeme zpět
convolved = np.fft.ifft(convolved_fft)

# nyní máme výsledek dlouhý fftsize, ale jenom část z něj je "same" (resp. "valid"). Vybereme tuto část.
convolved = convolved[len(coeffs)//2-1:len(chirp)+len(coeffs)//2-1]

print(np.allclose(convolved, filtered_shifted)) # True

Za povšimnutí stojí, že pokud aplikujeme stále stejný filtr na velké množství dat, tak nám ho stačí ztransformovat jen jednou na začátku a pak stále používat.

Co dělat, když data zpracováváme proudově, případně jsou tak dlouhá, že nemůžeme udělat jednu velkou FFT? K tomu se používá metoda overlap add, která umožňuje zpracovávat pomocí malých transformací postupně. Bohužel jsem ji nikdy osobně neimplementoval, tak se neodvažuji ji předvádět.

Decimace, podvzorkování (undersampling)

Nyní nejspíš máme signál, který je ofiltrovaný, a v části jeho spektra tak nic není. Decimací, tedy vyházením některých vzorků, tak můžeme snížit jeho vzorkovací rychlost.

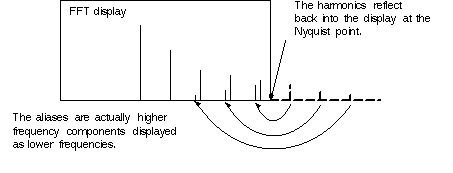
Teď to asi bude trochu mlhavé, protože úplně nevím jak to vysvětlit textem (na tabuli to jde líp), ale pokusím se. Pointa je, že spektrum signálu je jakoby periodické, nekonečně se opakující, a těmto věcem mimo „hlavní“ interval od -f_s/2 do f_s/2 se někdy říká spektrální repliky. Je to vidět na této ilustraci z již odkazovaného článku:

Nastavením vzorkovací frekvence jsme umístili značky na B/2, 3B/2, 5B/2 atd., kolem kterých se to neustále opakuje. Pokud vzorkovací frekvenci zvýšíme - tím, že mezi původní vzorky vložíme nuly - tak se nám jakoby zviditelní větší část tohoto myšleného spektra.

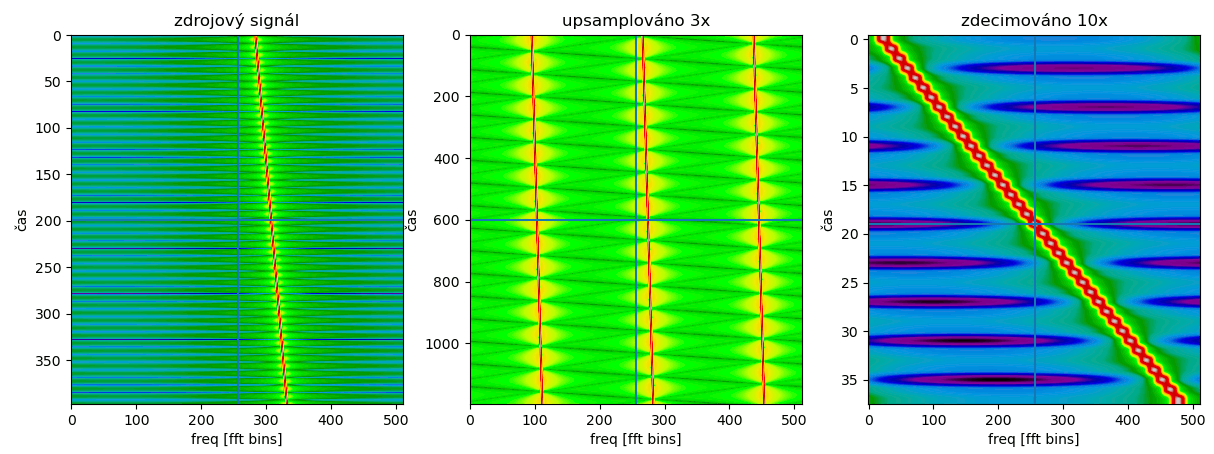
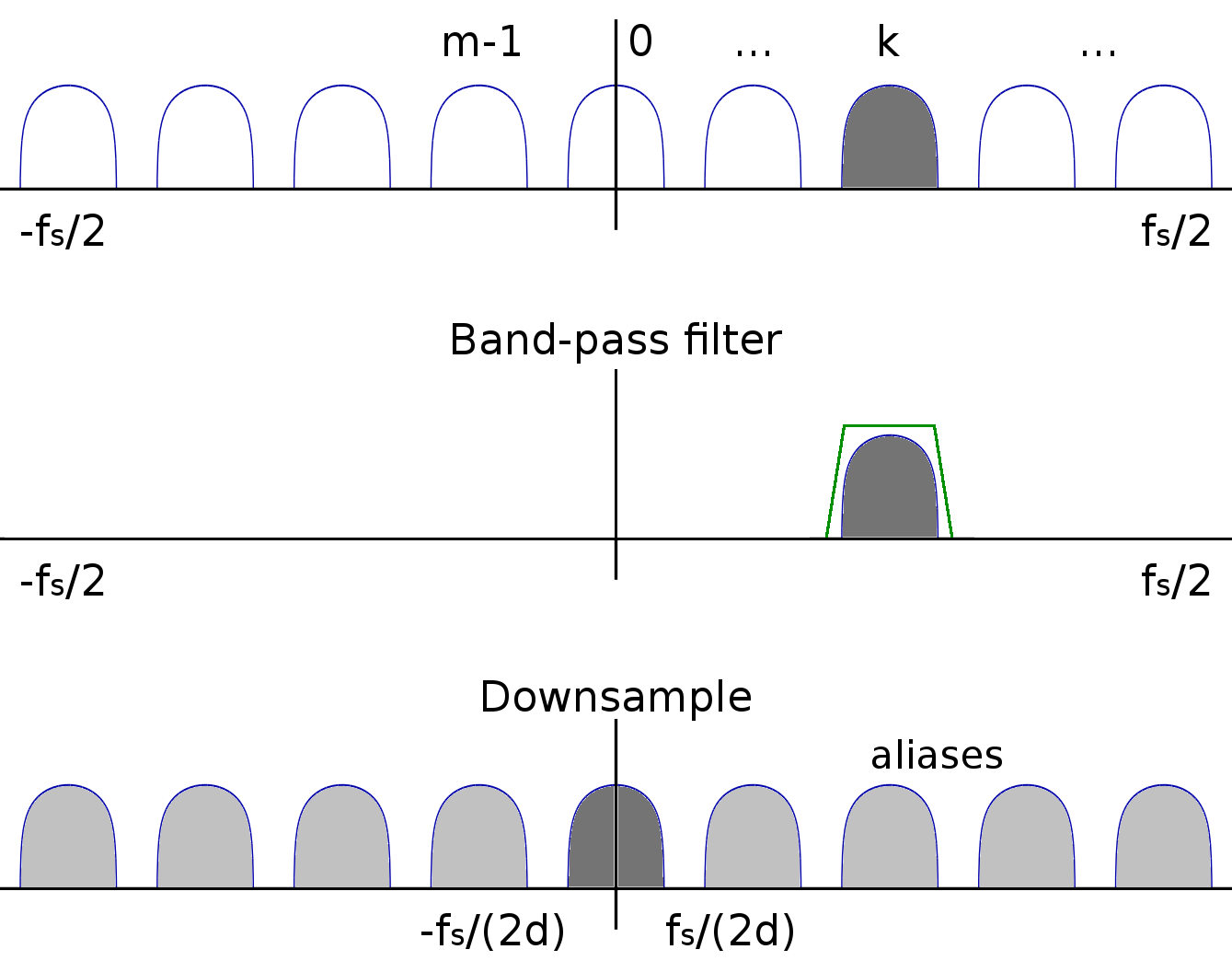
Pokud naopak vzorkovací frekvenci snížíme - například výše jsem ponechal jenom 1 z každých 10 vzorků (decim = chirp[::10]) - tak se nám značky B/2, 3B/2 atd. přeskupí a spektrální repliky se přeskupí podle nich - a vše, co tam bylo původně, se zamíchá do sebe. V případě výše je to v pořádku, protože signál byl pásmově omezený (bandlimited) a nově vzniklý signál tak neobsahuje žádný nežádoucí zamíchaný bordel, ale třeba na obrázku níže je příklad, který téměř určitě nechcete, případně je to hezky ilustrované tady.

Vybrání kanálu - možnosti

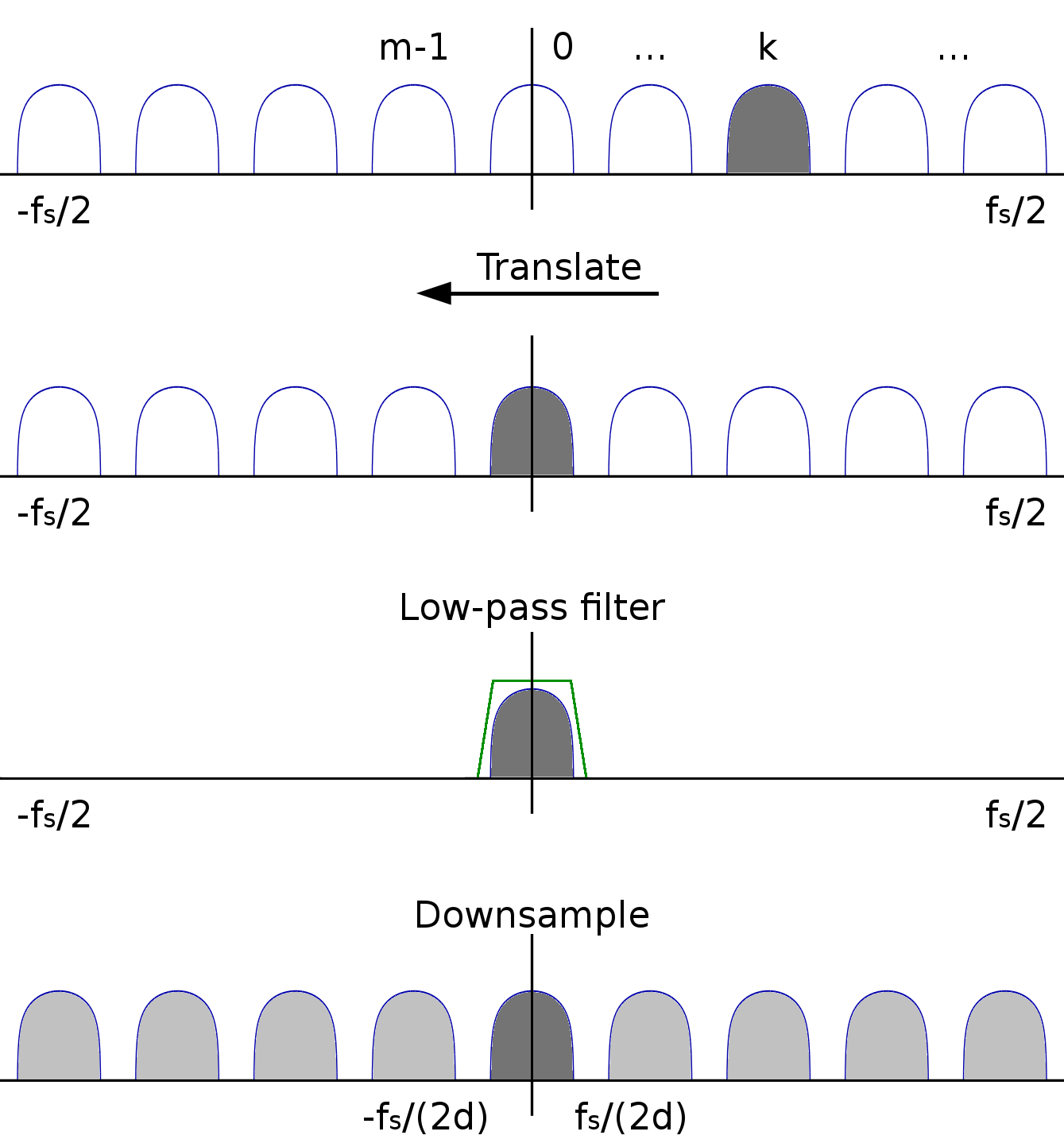
Vše uvedené by se hodilo nějak shrnout, uvést typický příklad, k čemu to použít. Typicky tedy řešíte, že máte nějaký signál, a teď z něj chcete vybrat kanál, zbytek zahodit a zdecimovat to na rozumnou vzorkovací frekvenci. Jaké tedy máte možnosti?

• Můžete to celé posunout rotátorem tak, aby kanál byl na nulové frekvenci, aplikovat lowpass a zdecimovat to. Zde je dobré si všimnout, že pokud budete lowpass aplikovat z definice, tak je zbytečné vyhodnocovat ho na všech bodech vstupního signálu, když hned v následujícím kroku provedete decimaci a část z nich zahodíte. Výhoda tohoto přístupu je, že lowpass je reálný, tedy odpadá komplexní násobení při jeho vyhodnocování. Nevýhoda je, že musíte rotátorem násobit celý vstupní signál.
  
• Můžete aplikovat bandpass, následně provést decimaci, a on se vám ten ofiltrovaný kanál nějak poskládá. Pokud se poskládal tak, že nemá nulovou frekvenci uprostřed, tak se rotátorem posune, aby měl. Zde je nevýhoda, že musíte bandpass aplikovat na celý vstupní signál (a navíc je komplexní), ale výhoda, že rotátor aplikujete až na zdecimovaný kanál. Pokud si navíc můžete použité frekvence zvolit sami, tak se to dá udělat tak, aby rotátor nebyl potřeba - zvolíte si je tak, aby po decimaci signál rovnou vyšel správně. Případný další podobný trik je, že se to zvolí tak, aby matice rotace obsahovala jenom jedničky a mínus jedničky (např. rotace o 90° taková bude, protože sin(90°)=1, cos(90°)=0) a rotátor tak znamenal pouze občasné násobení -1, což vlastně znamená jenom přehození znaménka.
  

       

Komentáře

[JiK]

jak ti houstne matematika, tak ti budou ridnout posluchaci a ctenari.

[🇨🇽]

eště to +- de :D

spíš víc by se hodilo mit ty skriptíky jakoby nějak rychle ke stažení git/zip/něco by se to nemuselo kopírovat :D ;D

[Miriam]

já tomu nerozumím a to je škoda asi si to budu muset víc nastudovat

[gsnak]

Toto je síce pekné ale ako vyrobím lacnú krabičku s jedným vstupom, jedným výstupom a 9V baterkou vnútri, zaujíma ma audio spektrum, tam asi python nepôjde.

[trekker.dk]

Máte pravdu. A dál?

[~]

co ti brani prepsat si to do rustu? neverim, ze bys o nem neslysel vzhledem k tomu ze to je nova odnoz vegansky sekty

[JiK]

Říká se, ze když se to přepíše do rustu tak prý už pak není potřeba ani ta 9V baterka do té jeho krabičky.

[Jendа]

Najdeš si implementaci FFT v jednom céčkovém souboru a budeš doufat, že to upočítáš na STM32 (ideálně ve fixed-point aritmetice, pokud to bude STM bez FPU). Zrovna jsem řešil, jestli takovou krabičku nepostavit, ale nechce se mi pálit čas kvůli neschopnosti státu.

[trekker.dk]

Odpověď "Chtělo by to opravdu kov.", když se mluví o hliníku, je lehce úsměvná...

ale nechce se mi pálit čas kvůli neschopnosti státu

Tak hlavně při té jízdě na červenou dejte pozor, abyste nevyhrál bouchalův pohár. Potichu jedoucí elektroauto je svině.

[JiK]

mam reseni. dej si za kolo vozik a na nej stary litinovy radiator. postaci prazdny, bez vody v nem. To bude jako blok motoru a smycka te detekuje

[🇨🇽]

tydlety návody hele a hele by nefungovali?? :O :O

[j]

Ehm, jenze ten semafor neni spatne nastavenej, ten je proste nefunkcni, protoze ten snimac muze fungovat maximalne jako doplnek, nikoli jako primarni zdroj informace. Takze ten smer by se mel v kazdym pripade rozsvecet v nejakym intervalu, bez ohledu na to jestli tam neco detekuje nebo ne.

A to nemluvim o odbocovaci sipce, ta specielne v praglu snad nefunguje spravne nikde. Oni totiz soudruzi nevedi, ze se nemuze a NESMI zhasinat samostatne. Protoze pak zakonite projedes na cervenou, protoze nemas sanci zastavit (natoz bezpecne).

---

Dete s tim guuglem dopice!

[Michal Kubeček]

Problém s opakovaným násobením nějakou maticí, přičemž výsledek má být vždycky jednotkový vektor (a mění se jenom jeho směr), je, že se vlivem nepřesností může tento vektor časem prodlužovat nebo zkracovat - spočítaná matice rotace může mít vlivem nepřesností třeba normu 0.99999 nebo 1.00001, takže vektor s každou iterací nepatrně natáhne nebo smrskne, a po výše zmíněném bilionu vzorků to naprosto ustřelí. Proto je potřeba vektor rotátoru občas normalizovat, tj. spočítat jeho skutečnou velikost a tou ho vydělit, čímž se z něj zase stane vektor jednotkový.

Nemáme ale úplně stejný problém i s fází? Tak jako se mi norma nepřenásobí úplně přesně jedničkou, nebude ani úhel otočení úplně přesně takový, jaký jsem chtěl, a při opakovaném násobení se ty chyby budou taky kumulovat. Nebo to u fáze nevadí?

[Jendа]

Alespoň já jsem zatím nikdy nepotřeboval, aby po X vzorcích bylo napočítáno ve fázi X*otočení_jednoho_vzorku.

[ampersand]

Proč lžeš?

[🇨🇽]

protože má pravdu :D :D ;D ;D

[vencour]

Aha. Teď mi došlo, že se píše o úpravě rozlišení (tj. převzorkování) za chodu. A že vlastně nevím, jaká citlivost na vstupu.
Ok, jsme uprostřed děje, něco z toho vyleze a bude zřejmě vysvětleno.
(A na DSP se ve volném čase taky podívám, co říkají nějaké podklady ...)

[Jendа]

No… spíš nebude. Teda můžu pak dát nějaký díl s příklady, ale tohle jsou obecné postupy co aplikuješ na svůj specifický případ.

A že vlastně nevím, jaká citlivost na vstupu.

Může tam být šmejdské rtl-sdr nebo frontend magnetické rezonance za několik mega.

[X]

Dalsi pecka. ale chtelo by to doplnit o prakticke pouziti, obrazky z HW, aby to nebyla jen teorie bez realneho ramce.

[안전놀이터추천]

I came here after searching for 안전놀이터 to spend my time more efficiently after work. The content is not burdensome and the writing is easy to understand. Thank you so much for being able to spend meaningful time after work.