DSP kuchařka: počítáme spektrogram (waterfall)

9.8.2021 06:06 | Přečteno: 4216× | Meteopress | | poslední úprava: 6.8.2022 13:58

Pro debugování jakéhokoli systému zpracovávajícího rádiové signály se extrémně hodí umět si nakreslit waterfall (a.k.a. spektrogram či Short-time Fourier transform), který zobrazí, jaké frekvence se v jakém čase v signále vyskytují.

Začíná seriál DSP kuchařka o zpracování číslicových signálů, zaměřený především na rádiové signály. Je to kuchařka, ne rigorózní výklad, sorryjako. Příklady programů budou především v Pythonu, ale pro skutečné nasazení to nejspíš budete muset napsat v něčem rychlejším, třeba v C podle návodu co vyšel minule.

Úvod - komplexní signály

Na rozdíl od zvuku, kde se pracuje s reálnými vzorky, které vyjadřují něco jako okamžitý tlak vzduchu v daném čase, se u rádií signál reprezentuje komplexními vzorky. V počítači se reprezentují nejčastěji dvojicí (reálná část, imaginární část), označováno jako I a Q, nicméně při uvažování o problémech bývá užitečnější se na to dívat jako na dvojici (amplituda (absolutní hodnota), fáze) (označováno většinou r a phi). Na první pohled se může zdát použití komplexních čísel jako zbytečná komplikace - z antény nám přece vede jeden drát, na kterém je reálné napětí - ale věřte mi, je to opravdu mnohem lepší než se snažit provádět výpočty s reálnými čísly. Detailní popis naleznete třeba v článku tady, ilustrované příručce tady a nekonečném množství zdrojů tady. Několik bodů nutných pro tento zápisek:

• U reálného signálu po jeho navzorkování rychlostí f_s získáme signál s frekvencemi od 0 do f_s/2, pokud si zkusíte nakreslit „rychlejší sinusovku“ a „položit na ni vzorky“, zjistíte, že pro f_s/2 leží všechny na přímce (tj. nedokážeme takový signál odlišit od stejnosměrného) a pro vyšší navzorkujeme sinusovky s frekvencemi zase od nuly. Animace, obrázek.

  (Zatím ignorujeme úmyslné podvzorkování a periodičnost spektra, to budeme řešit v příštím díle.)

• U komplexního signálu vzorkovaného rychlostí f_s získáme frekvence od -f_s/2 do +f_s/2, což tedy neznamená, že jsme ušetřili hardware, zase potřebujeme dvoukanálový převodník, ze kterého lezou I a Q složky, nebo 2x rychlejší jednokanálový a komplexní signál z toho udělat softwarově. Intuice za zápornými frekvencemi je taková, že vzorkujeme polohu bodu v komplexní rovině, a ten může obíhat buď po směru, nebo proti směru hodinových ručiček, a to je kladná, nebo záporná frekvence.

  

Fourierova transformace

Pojmy

• Fourierova transformace je krabička, do které se vloží funkce R→C (jedna z fyzikálních představ je funkce čas → komplexní hodnota signálu) a vypadne z ní jiná funkce R→C (fyzikální představa: frekvence→(amplituda a fáze)) podle vzorečku, který si můžete přečíst na Wikipedii. „Defaultní“ je spojitá Fourierova transformace (nekonečné spojité funkce a vzoreček s integrály), které se většinou říká prostě jen Fourierova transformace, a používá se především při teoretické analýze a my ji používat nebudeme.
• Diskrétní Fourierova transformace (DFT) je krabička, do které se vloží funkce N→C (představa: pole komplexních vzorků) a vypadne z ní jiná funkce N→C (tj. opět pole komplexních vzorků). Někdy se definuje pro nekonečné vektory (což se opět používá pro analýzu), ale takovým hackem (prohlásíme, že vstup je všude jinde nulový) se dá definovat pro vektory konkrétní délky. To je to, s čím se pak počítá v počítači, máme pole komplexních čísel, ztransformujeme ho a dostaneme jiné pole komplexních čísel.
• Obě transformace mají i k sobě inverzní transformaci (inverse DFT, IDFT). Respektive tak, jak se to většinou definuje a implementuje, pokud spočítáte DFT z dat velikosti N a z toho IDFT, dostanete původní data, ovšem N-krát větší. Pokud vám to vadí, je potřeba výsledek vydělit N, respektive po transformaci tam i zpět odmocninou z N.
• Rychlá Fourierova transformace je rodina algoritmů pro asymptoticky rychlé počítání DFT. DFT implementované naivním způsobem má časovou složitost O(N²), FFT využívá trik, pomocí kterého to lze spočítat v O(NlogN). Algoritmus je praktický, tj. má rozumné konstanty a běží rychle na skutečných počítačích. Pro praktické použití je důležité, že FFT algoritmy nejrychleji fungují, pokud je velikost vstupu číslo, které lze rozložit na součin pouze mnoha malých prvočísel. Ideální je mocnina dvojky (např. 1024), relativně použitelná jsou i čísla, u nichž se v rozkladu občas objeví 3, 5, 7… (např. 3*1024 = 3072), velmi špatná jsou velká prvočísla. Pokud si můžete velikost počítané transformace volit (často to jde za cenu toho, že třeba vstup doplníte nulami), je nejlepší zvolit nejbližší vyšší mocninu dvojky.

FFT se dá používat ke dvěma věcem (a určitě i mnoha dalším):

• Použijeme přímo fyzikální interpretaci výsledku, tj. že na vstupu je čas a na výstupu je frekvence, protože přímo chceme dělat něco s časem a s frekvencemi. To budeme řešit dnes.
• Máme nějaký problém, který s tímto nesouvisí, a pro který máme pomalý algoritmus. Podaří se nám problém přeformulovat tak, aby šlo aplikovat DFT, provést nějaký rychlý mezivýpočet, a pak aplikovat inverzní DFT. Díky rychlému spočítání pomocí FFT tak problém vyřešíme rychleji. To budeme řešit v nějakém příštím díle.

Spektrum

Co se stane, když do FFT strčíme kousek navzorkovaného komplexního signálu (délky N)? FFT počítá tohle:

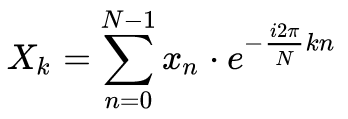
Tj. pro každý prvek výstupu (k) to projde celý vstup (postupně všechny prvky x_n - proto má také naivní implementace složitost O(N²)) a vynásobí ho to nějakou zběsilostí, která se postupně mění podle n (ještě je tam N, to je konstanta - zvolili jsme si ji tím, jak dlouhý signál jsme do toho vložili; k, což záleží na tom, na který prvek výstupu se zrovna koukáme; 2π, což je úplně konstanta, a i, což vyřešíme právě teď). Jak vypadá e^{-i*postupně_se_zvětšující_číslo}? Je to komplexní číslo a nakreslíme si ho v komplexní rovině:

import numpy as np
import matplotlib.pyplot as plt

args = np.linspace(0,6,30)
e = np.exp(-1j*args)
x = np.real(e)
y = np.imag(e)
plt.scatter(x, y)
for i in range(len(args)):
  plt.annotate("e^-i*%.2f"%args[i], (x[i], y[i]))
plt.axvline(0)
plt.axhline(0)
plt.show()

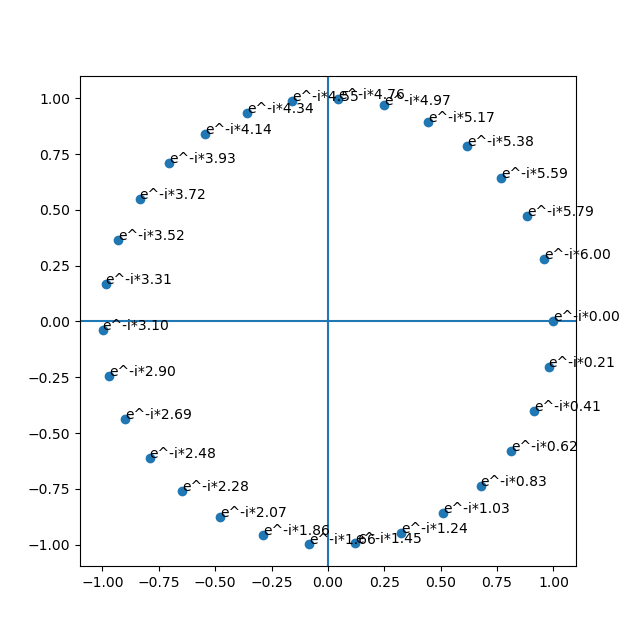
Je to tedy něco, co postupně rotuje po jednotkové kružnici, jako na tom obrázku z úvodu. (této věci se taky říká rotátor) Pak tam jsou ještě ty škálovací faktory - konkrétně k, které říká, jak rychle to má rotovat. Tedy vlastně v různých prvcích výstupního pole bude vynásobení vstupního signálu s různě rychle rotující komplexní exponenciálou. A co vlastně znamená tohle násobení po prvcích? No, pokud si signály „budou podobné“, tak se vždycky bude násobit velké kladné číslo s velkým kladným číslem, velké záporné číslo s velkým záporným číslem, malé číslo s malým číslem atd. a když se to všechno sečte, tak výsledkem bude velké číslo. Naopak pokud si podobné nebudou, tak se budou násobit různá náhodná čísla mezi sebou a výsledek bude „skoro nula“ protože se to navzájem vyruší. V každém prvku výstupu je tedy napsáno, jak moc si je vstup podobný s rotátorem o nějaké frekvenci. A ještě tím, jak je to celé komplexní, tak tam ve skutečnosti je absolutní hodnota - jak moc jsou si absolutně podobní - a fáze - jak moc jsou navzájem posunutí.

Ještě je potřeba trochu dořešit jednotky. n/N je číslo, které jde od 0 do 1, protože n jde od 0 o N (resp. do N-1, ale whatever). Pak tam je 2π, protože exp vyžaduje argument v radiánech, tak aby byla jedna otáčka od 0 do 2π. A pak je tam ještě k, což je tedy rychlost rotátoru v daném prvku výstupu. Pro k=1 to udělá jednu otočku (celý argument exp pojede od 0 do 2π), dalo by se tedy říct, že to odpovídá frekvenci 1 (myslete si třeba 1 Hz, ta věc samozřejmě neví vůbec nic o parametrech vašeho systému, takže pokud chcete znát konkrétní frekvence, musíte si to přepočítat). Pro k=2 to udělá za stejnou dobu dvě otáčky (od 0 do 4π; 2 Hz). Pro k=3 by to udělalo 3 otáčky atd. Co se ale stane, až dojedeme do půlky (k=N/2)? Rotátor se už točí tak rychle, že za jeden časový krok udělá více než polovinu otáčky, a dojde k aliasingu jako jsem ukazoval na začátku nebo jako když je ve filmu záběr na kolo rychle jedoucího auta, a zdánlivě to bude vypadat, jako kdyby se točil opačným směrem. Takže to do druhé poloviny vlastně nasype podobnost se zápornými frekvencemi.

No a pak tam je ještě celou dobu to mínus, protože to tak někdo definoval a tak to prostě je, jinak by se to točilo na druhou stranu.

fftshift

Výsledek tedy vypadá tak, že první (nultý) prvek odpovídá nulové frekvenci („DC“), pak to stoupá do poloviny do f_s/2, pak se to překlopí na -f_s/2 a pak to zase stoupá k nule. Tohle je pro některá využití nepříjemné, protože když na to lidi koukají, tak by spíš chtěli mít to od -f_s/2 do f_s/2 a nulu uprostřed. Takže se někdy půlky toho výstupního pole prohodí. V numpy je na to funkce fftshift.

Okýnkování (windowing)

Vstupní signál, který budeme pomocí FFT analyzovat, bude vždycky konečný:

• Máte třeba nahrávku v nějakém souboru a ten je prostě nějak dlouhý.
• Máte nějakou dlouhou nahrávku a víte, že třeba mezi časy 3.05 sekundy a 3.1 sekundy nastal fyzikální jev, který chcete zkoumat, a zbytek nahrávky by jenom rušil. Takže to dokonce budete muset nějak vyseknout z existující nahrávky.
• Máte dlouhou nahrávku a počítat příliš velké FFT je nepraktické (nevejde se to do paměti, dlouho to trvá a tak) a dostanete výsledek s absurdně velkým rozlišením.

Nejjednodušší možnost samozřejmě je vzít ty samply z rozsahu co nás zajímá a s tím pracovat. To má ovšem nevýhodu v tom, že to má ostrý začátek a ostrý konec, a signál jakoby z nuly skočí přímo na nějakou hodnotu. Tento náhlý skok, diskontinuita, se projeví ve výsledné frekvenční analýze jako jakýsi šum, spousta různých frekvencí, které v originále ve skutečnosti nebyly. Proto se téměř vždy používá nějaké okno, což je funkce, která amplitudu signálu na začátku plynule zvýší a na konci zase plynule sníží do nuly a nedochází tak k náhlým skokům.

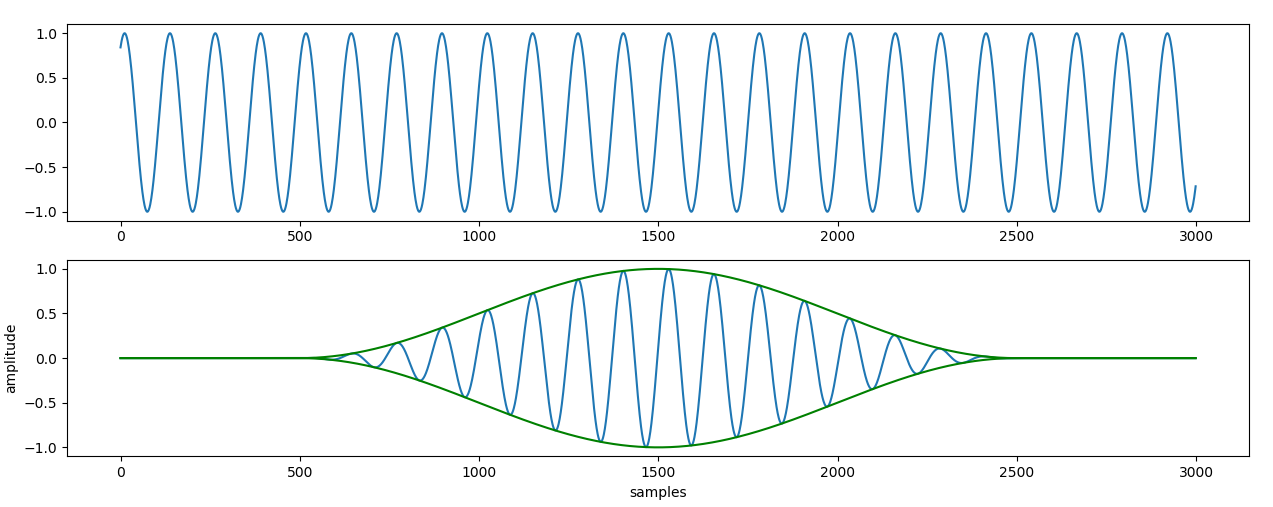
Nevýhodou pro změnu je, že jsme takhle přišli o nějakou informaci na krajích zkoumané oblasti, a frekvenční rozlišení výsledku nebude tak ostré (protože máme jakoby menší interval kde můžeme frekvenci měřit) Pokud tedy v signálu je někde jedna osamocená dominantní frekvence, tak se rozprskne do několika sousedních prvků výsledku; na druhou stranu, pokud tam byla frekvence, která by padla přesně mezi dva prvky výsledku (např. 20.5 Hz a naše rozlišení je po 1 Hz) a do žádného z nich pořádně, tak tohle to opraví.

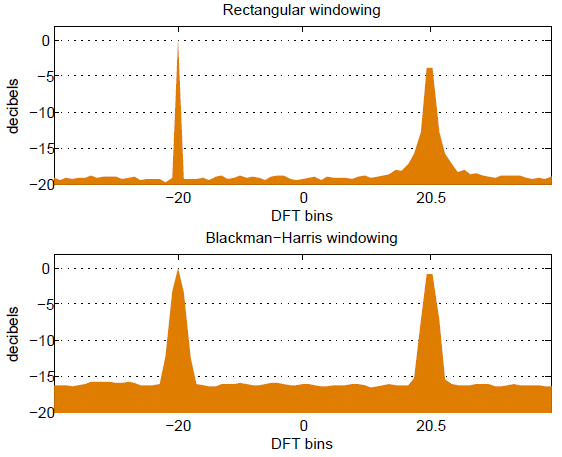
Na Wikipedii najdete hromadu různých okýnek, která jsou zvolena kompromisně mezi tím, kolik užitečného signálu nám zůstane a jak pozvolný je náběh. Osobně to neřeším a všude používám Hammingovo, a když mám pocit, že se to s ním rozbilo, tak Hannovo.

Realizace, spektrogram

Načtení dat

Setkal jsem se se 3 formáty, které se používají pro ukládání rádiových signálů.

• cfile. Tento formát se používá pro samotné zpracování signálu a pro reprezentaci a ukládání mezivýsledků. Jedná se o za sebou jdoucí floaty (32bit, jednoduchá přesnost), vždycky jeden reprezentuje I složku a druhý Q složku. V NumPy tomu odpovídá formát np.complex64, v C complex float. Endianita se používá nativní, ale protože všichni mají little endian počítače, tak je to prostě little endian a tečka. Formát nemá žádná metadata (vzorkovací frekvence…), je to prostě soubor s vysypanými floaty. Osobně ukládám kratší metadata do názvu souboru, delší do souboru se stejným názvem a jinou příponou bokem. Výhodou formátu je dynamický rozsah a přesnost, nevýhodou poměrně velká velikost (na každý vzorek padne 8 bajtů).
• i16. Za sebou jdoucí int16_t, opět jeden I a jeden Q. Tento formát používá například bladeRF a s některým nastavením AirSpy.
• u8. Za sebou jdoucí uint8_t, jeden I a jeden Q. Tento formát používá rtl-sdr. Je bez znaménka, takže je s offsetem a při jeho načítání tak je potřeba odečíst 127.5.

Takhle načteme cfile:

samples = np.fromfile("soubor.cfile", dtype=np.complex64)

S těmi dalšími je to horší, protože NumPy nemá komplexní intové typy, a navíc to stejně chceme převést do floatů, aby s tím šlo počítat. V céčku prostě načtu do bufferu int16_t a pak ve smyčce přiřazuju do pole floatů a pak to třeba přetypuju na complex float a ono se to stane samo. V NumPy:

samples = np.fromfile("soubor.i16", dtype=np.int16).astype(np.float32).view(np.complex64)

Pokud nemáte soubor na vyzkoušení, tak nahrávku z rtl-sdr ve formátu u8 jsem dealoval v předchozím zápisku. Můžete si ji stáhnout zde. Načteme ji tedy:

samples = np.fromfile("fm.bin", dtype=np.uint8) - 127.5
samples = samples.astype(np.float32).view(np.complex64)

Můžeme se podívat, jak to vypadá a že data dávají smysl (jsou to nějaké vlny, v očekávaném rozsahu zhruba -128 až 128).

import matplotlib.pyplot as plt
plt.plot(np.real(samples[:10000]))
plt.plot(np.imag(samples[:10000]))
plt.show()

Vezmeme z toho začátek (třeba 1024 vzorků - rozumná mocnina dvojky), vyrobíme si okýnko, ztransformujeme a nakreslíme absolutní hodnotu.

win = np.hamming(1024)
sample = samples[:1024] * win
res = np.fft.fft(sample)
plt.plot(np.abs(res))
plt.show()

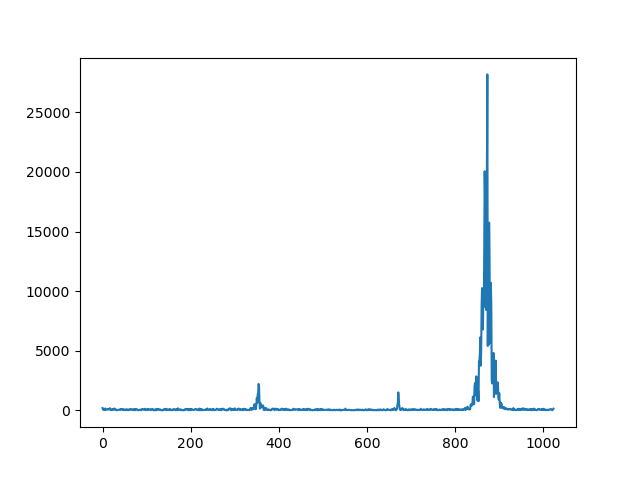
Výsledek je poněkud meh, protože hodnoty mají moc velký rozsah, což vyřešíme za chvíli zlogaritmováním. Ale něco to dělá.

Spektrogram

Praktičtější, a minimálně pro mě vizuálně mnohem srozumitelnější, je kreslit 2D obrázek. Na jedné ose budou frekvence, na druhé ose bude čas, a barva obrázku bude kódovat výsledek FFT (resp. jeho absolutní hodnotu). Tak je vidět vývoj situace v čase. Pokud jste někdy viděli Gqrx nebo podobný software, tak tohle je přesně to, co zobrazuje. A waterfall se tomu říká, když to nahrává signál, v reálném čase ho to kreslí a stará data to posouvá dolu.

Jako první vyřešíme, jaké hodnoty budeme zobrazovat. Typicky se počítá logaritmus čtverců: 20*log10((Re2+Im2)/fftsize). Dělí se to velikostí transformace, protože FFT výsledek natahuje, jak jsem již zmínil. A pak se to ještě násobí 20 a výsledek jsou přímo decibely, což je praktické.

Dále si musíme vymyslet časové a frekvenční rozlišení. To záleží čistě na konkrétní aplikaci a volí se podle toho velikost transformace (větší transformace samozřejmě zvýší frekvenční rozlišení, ale zhorší časové, protože se kouká na delší časový úsek najednou a v rámci tohoto úseku již nejde rozlišit různé časy) a případně overlap, tj. překryv okýnek položených vedle sebe (ten je ale většinou rozumné nastavit na 0.5, tj. další okýnko vždy pokládáme tak, aby se polovinou krylo s předchozím, díky čemuž tak nějak rozumně zachytíte něco, co třeba zrovna vyšlo přesně na kraj jednoho a zrovna je to tak v místě, kde je okýnko skoro nulové). Pokud naopak chcete časové rozlišení nižší, tak se průměruje vždycky několik výsledků po sobě. Asi by se to mělo průměrovat před zlogaritmováním. No a pak se ještě občas průměruje ve směru frekvence (tj. například spočítáte FFT velkou 2048, ale kreslíte to jenom 1024 pixelů široké), protože vlivem okýnka je to trochu rozmazané a tohle tomu pomůže.

No a pak se ještě udělá fftshift, aby byla nulová frekvence uprostřed, a to je všechno. Tohle to celé vyrobí:

fftsize = 1024
win = np.hamming(fftsize)
output = []
for i in range(0, len(samples)-fftsize, fftsize//2): # posouváme se vstupním polem vždy o fftsize/2 vzorků = overlap 0.5
  data = samples[i:i+fftsize] * win
  transformed = np.fft.fft(data)

  power_spectrum = 20*np.fft.fftshift(np.log10((np.square(np.real(transformed))+np.square(np.imag(transformed)))/fftsize))

  output.append(power_spectrum)

plt.imshow(output, aspect='auto', cmap="nipy_spectral")
plt.show()

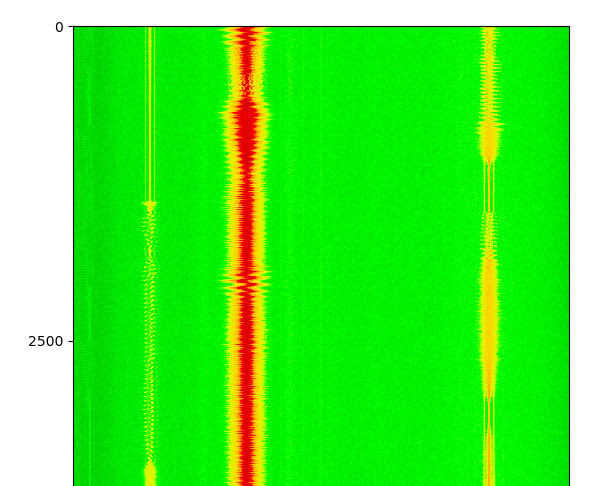
Výsledek vypadá podobně tomuto obrázku ze zápisku o GNU Radiu, no aby taky ne, když jsme spočítali to stejné, akorát tady s vyšším časovým rozlišením.

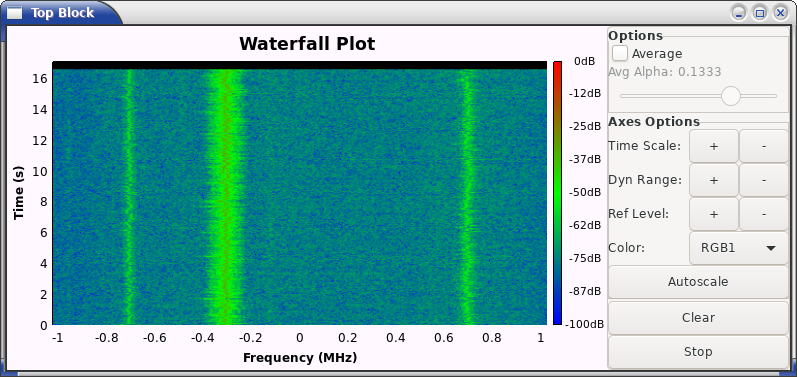
Vidíme tam tři stanice, jednu silnou a dvě slabší. Na té silné je nějaký provoz a na těch slabších je asi řeč, protože jsou tam vidět pauzy kdy se nic nevysílá (to časem nakoukáte…). Co si konkrétně ze spočítaného spektrogramu odnést záleží opravdu na tom, co zrovna děláte. Můžete takhle dělat reverzní inženýrství neznámého komunikačního protokolu, hledat rušení a zjišťovat, jestli je časově nebo frekvenčně omezené a tedy zda by šlo potlačit, nebo pokud sami signál generujete, tak si kontrolovat, jestli opravdu vypadá tak, jak si představujete.

Random příklad: LoRaWAN

Na internetu si přečtete, že LoRa (fyzická vrstva, kterou používá síť LoRaWAN, což je bezdrátová síť určená pro posílání párbajtových zpráv každých několik minut a je optimalizovaná na nízký odběr energie) kóduje jedničky a nuly pomocí upchirpu a downchirpu, což zároveň slouží pro rozprostírání spektra. Na spektrogramu mi to pak nekreslilo takovéto krásné patterny:

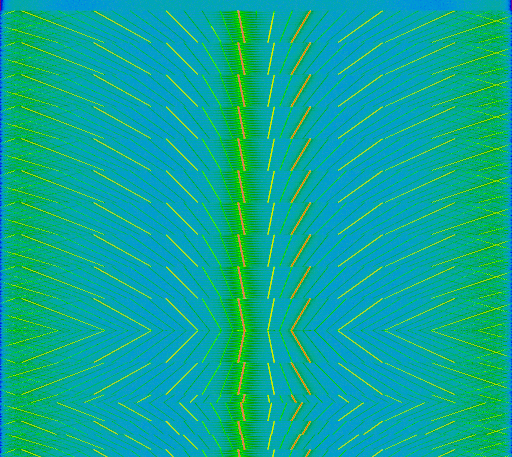
Hned tu vidíme druhý efekt, to, že tam toho je takhle strašně moc a ještě se to zrcadlí kolem nulové frekvence značí, že byl vstupní signál strašlivě silný, resp. byl nastavený strašně velký zisk ve vstupním zesilovači rádia, a došlo k brutálnímu zkreslení.

V tomto konkrétním případě šlo o mrtvé lorawanové zařízení, o kterém dodavatel tvrdil, že jemu funguje, zatímco nám nešlo registrovat do sítě. Porovnáváním záznamů z funkčního kusu a z tohoto jsme zjistili, že vysílaný signál je mnohem slabší (i když to zrovna z tohoto obrázku nevypadá ), což jsme následně ověřili fyzicky přímo vedle lorawanové gatewaye (kde to fungovalo v pořádku - asi na 30 metrů).

       

Komentáře

[Gréta]

supr vodopád :D ;D

[kreta]

co to asi kresli v miste vpichu vakciny ovecek?

OFDM modulaci.

[Max]

Moc pěkný, díky. Apropo, co používáš za hw na to měření?
Díky
Zdar Max

[Jendа]

Teď stavím úplně vlastní radar from scratch (tj. chceme zahodit ty přebastlené lodní radary) a tam používám bladeRF (a ano, bude o tom writeup - minulý víkend se mi to totiž konečně podařilo rozchodit \o/). A ten signál LoRaWAN je taky změřený tím, ale šlo by použít cokoli jiného, protože 868 MHz podporuje kde co. Pokud řešíš pouze příjem a chceš něco lepšího než rtl-sdr, tak doporučuji AirSpy.

[Jendа]

Twitter thread (ano, nepochopil jsem, jak fungují thready, a zaspamoval jsem tím hlavní timeline :/)

[Miriam]

ty pičo Jenda staví vlastní radar, čumím! Respekt lvl maximální! Díky za pěkný zápisek

[AsciiWolf]

Skvělý blogpost, ten klidně mohl vyjít jako článek. Díky!

[JiK]

co kdyz transformujes neco co neni komplexni, treba skutecne to audio (sonar)?

[Jendа]

Převedeš to na komplexní čísla, přičemž do imaginární složky dáš nuly, a po transformaci zahodíš tu polovinu se zápornými frekvencemi. (existuje i nějaký trik, jak ušetřit polovinu procesorového času (protože tady zbytečně počítáš něco, co zahazuješ), ale zapomněl jsem ho)

[MarV]

Ušetřit výpočetní čas pro reálné signály lze:

1. Počítat jedním FFT dva reálné signály zároveň. Místo nulama se komplexní signál sestaví ze dvou nezávislých bloků dat. FFT se vypočítá standardím způsobem a nakonec se výsledky oddělí na základě vlastností symetrie spektra reálného signálu. Tzv. doubling algorithm.
2. Signál se rozdělí na sudé a liché vzorky. Sudé se použijí jako reálná složka a liché jako imaginární. Opět se vypočítá standardní FFT a výsledek se další matematickou magií zase složí dohromady jako jedno spektrum. Tzv. packing algorithm.

Jinak existuje spousta jiných optimalizací výpočtu ...

[rad]

Jen malá poznámka.

Ona ani elektromagnetická vlna není 'komplexní'. Termíny 'komplexní' a 'reálný' patří do matematiky a nemají přímou vazbu na konkrétní fyzikální veličiny.

Elektromagnetické vlnění je bez problému možné popsat čistě reálnými funkcemi (už proto, že řešením vlnové rovnice jsou obecně harmonické funkce). Důvod proč při popisu používáme zbytečně redundantní tzv. komplexní analytický signál spočívá v tom, že nám tento formalizmus umožňuje mnohem elegantnější a jednoduší analytické zpracování. Ve výsledku je potřeba ale vždy tuto redundanci odstranit a omezit se pouze na reálnou složku tohoto komplexního analytického signálu.

[⧠ A = 0]

Docela bych chtěl vidět dejme tomu kvantovou teorii pole bez komplexních čísel.

[Michal Kubeček]

Ono se dá udělat ledacos. Co si tak vzpomínám, Jarník má větu o implicitních funkcích (formulaci i důkaz) natvrdo v soustavách rovnic, bez náznaku nějaké maticové nebo vektorové symboliky. Je to naprosto nepřehledné a nestravitelné, ale formálně je to správně. Takže i ta kvantovka by se určitě - technicky - dala popsat bez použití komplexních čísel. Jestli by to mělo i jiný smysl než teoretické cvičení, to je samozřejmě jiná otázka (a odpověď je asi celkem jasná).

[⧠ A = 0]

Vtip je v tom, že s komplexními Hilbertovými prostory obvykle pracuje přímo axiomatika kvantové mechaniky (narozdíl od klasické teorie pole, kde si člověk vskutku může vcelku vystačit s reálným popisem; komplexní čísla se objevují až s Fourierovou transformací, ale jak bylo řečeno, ta se dá udělat i reálná). Takže by mě zajímalo, zda je možné udělat nějakou verzi axiomatiky kvantovky bez komplexních čísel (aby to ovšem zároveň nebyla vyloženě nějaká jejich emulace).

[Michal Kubeček]

Cokoli, co lze zapsat pomocí komplexních čísel, se dá rozepsat i bez nich, prostě se to rozepíše na reálnou a imaginární část. Bude to podstatně méně přehledné, nebude v tom tak dobře vidět ta logika, ale čistě technicky to udělat jde.

[⧠ A = 0]

Já vím, však proto taky píšu

aby to ovšem zároveň nebyla vyloženě nějaká jejich emulace

[kralyk z abclinuxu]

Vtip je v tom, že s komplexními Hilbertovými prostory obvykle pracuje přímo axiomatika kvantové mechaniky

Nerozumim tomu, tak se možná zeptám úplně blbě: Je pro kvantovku podstatný, že imaginární část je násobek i a má to nějaké s tim spojené vlastnosti, nebo jsou to jen glorifiovaný 2d vektory?

[Heron]

Komplexní čísla rozhodně nejsou vektory. Komplexní čísla jsou zejména o rotacích a v některých interních zákonech zachování (symetriích) - kalibrační symetrie pole se mění jen fáze. Hodnota (velikost) se nemění a na venek to vypadá vlastně stejně, přesto pro některé interakce to má významný vliv - vhodnou kalibrační symetrií vlastně vznikají některá fyzikální pole.

Jako určitě by šlo simulovat komplexní čísla bez komplexních čísel čistě pomocí rotačních matic pro transformace vektorů, ale byla by to totálně zbytečná vrstva navíc. (Takhle nějak AFAIK vznikala první teorie silné interakce, všude matice rotační transformace, až to někomu přišlo divné, tak to prohlásil za posun fáze pole nebo tak něco.)

[rad]

Jak psal Michal Kubeček, udělat je možné všechno. Matematiku je potřeba chápat jen jako jazyk popisující určitý fyzikální systém. A způsobů jak takový systém popsat bude asi existovat v principu nekonečně mnoho. Pakliže jsou ale všechny ekvivalentní (což musí, mají-li být správné) je asi možné každý z nich považovat za určitou emulaci ostatních.

Jinak v klasické elektrodynamice se (ve standardním formalizmu) 'neobjevují komplexní čísla s Fourierovou transformací', nýbrž jsou úměle zavedena hned na začátku při řešení Maxwellových rovnic právě pro snazší analytická řešení.

[⧠ A = 0]

Jinak v klasické elektrodynamice se (ve standardním formalizmu) 'neobjevují komplexní čísla s Fourierovou transformací', nýbrž jsou úměle zavedena hned na začátku při řešení Maxwellových rovnic právě pro snazší analytická řešení.

... čili nikoliv hned na začátku, nybrž až při řešení soustavy lineárních differenciálních rovnic pomocí Fourierovy transformace

Maxwellovy rovnice jako takové žádné komplexní členy neobsahují (a řešení jsou taky obvykle potřeba reálná), zatímco i pitomá Schrödingerova rovnice má v sobě rovnou imaginární činitel.

[rad]

čili nikoliv hned na začátku, nybrž až při řešení soustavy lineárních differenciálních rovnic pomocí Fourierovy transformace

Z pohledu teorie elektromagnetického pole je řešení soustavy Maxwellových rovnic opravdu úplný začátek. Navíc standardně se postupuje tak, že se nejprve odvodí vlnová rovnice (hyperbolická parciální rovnice druhého řádu) a ta se následně řeší (obecně) separací proměnných.

Maxwellovy rovnice jako takové žádné komplexní členy neobsahují (a řešení jsou taky obvykle potřeba reálná), zatímco i pitomá Schrödingerova rovnice má v sobě rovnou imaginární činitel.

Jenže to je právě pouze otázka použitého formalizmu. I Maxwellovy rovnice je možné vyjádřit ve formě komplexních operátorů. A stejně tak i (některé, viz dále) kvantově mechanické systémy je možné popsat bez použití aparátu komplexnich čísel tak, že se bězně používaný komplexní Hilbertův prostor zamění za prostor reálný o vyšší dimenzi.

Nicméně jsem díky tomu narazil na zajímavý článek, který doporučuji (minimálně úvod a závěr): Quantum physics needs complex numbers (https://arxiv.org/pdf/2101.10873.pdf). Řeší tam otázku, zda jsou komplexní čísla v kvantové teorii jen a convenient mathematical tool or an integral part of the theory. A dochází tam ke stejnému závěru co ty. Nicméně ta argumentace je o něco komplikovanější než že ve Schrödingerově rovnici je imaginární jednotka.

Člověk se pořád učí. Útěchou mi může být fakt, že: The occurrence of complex numbers within the quantum formalism has nonetheless puzzled countless physicists, including the fathers of the theory, for whom a real version of quantum physics, where states and observables are represented by real operators, seemed much more natural.

[S.B.]

Pardon, netvrdim, že všemu rozumim, všiml jsem si nějaké "použitelnosti" (že to něco dělá) u nastavení RBW a VBW (viz např. zde), mají nějakou souvislost s Tvou implementací?

[Jendа]

Já to pochopil jako RBW = velikost binu FFT (respektive několika sousedních binů, protože vlivem okýnka je to mázlé typicky tak přes 3-4 biny). U hardwarového spektráku to navíc určuje refresh rate a vybíráš si to proto, že někdy tě zajímá široké pásmo a potřebuješ rychlý refresh, protože tím měříš živé zařízení, které ladíš. A VBW = výsledek projedeme třeba rolling average filtrem.

[S.B.]

Já jen vim, že nastavení zobrazení (vzorkování?) má vliv na to, co mi vyleze, co dostanu. Asi to je vyšší dívčí. Lepší hw spektráky pak i zvládnou naladit vlastní refresh, nezávisle na filtru pro "data".

[ja osobne]

Jendo, aky mas nazor na toto ?

[panpanik]

me presvedcily testimonialy dole, jak nekdo zacne samou radosti recitovat lorem ipsum, tak to musi bejt superskvely

a diky jendovi za super pocteni

[/dev/win]

možno si to ešte nikto nekupil

[Jendа]

Já pro to nemám use-case, ale asi dobrý.

[AsciiWolf]

To je nějaká kopie Flipper Zero nebo scam?

[X]

Jsi fakt borec Jendo. Opet paradicky, diky!