Byla vydána nová verze 1.12.0 dynamického programovacího jazyka Julia (Wikipedie) určeného zejména pro vědecké výpočty. Přehled novinek v příspěvku na blogu a v poznámkách k vydání. Aktualizována byla také dokumentace.
V Redisu byla nalezena a v upstreamu již opravena kritická zranitelnost CVE-2025-49844 s CVSS 10.0 (RCE, vzdálené spouštění kódu).
Ministr a vicepremiér pro digitalizaci Marian Jurečka dnes oznámil, že přijme rezignaci ředitele Digitální a informační agentury Martina Mesršmída, a to k 23. říjnu 2025. Mesršmíd nabídl svou funkci během minulého víkendu, kdy se DIA potýkala s problémy eDokladů, které některým občanům znepříjemnily využití možnosti prokázat se digitální občankou u volebních komisí při volbách do Poslanecké sněmovny.
Společnost Meta představila OpenZL. Jedná se o open source framework pro kompresi dat s ohledem na jejich formát. Zdrojové kódy jsou k dispozici na GitHubu.
Google postupně zpřístupňuje českým uživatelům Režim AI (AI Mode), tj. nový režim vyhledávání založený na umělé inteligenci. Režim AI nabízí pokročilé uvažování, multimodalitu a možnost prozkoumat jakékoliv téma do hloubky pomocí dodatečných dotazů a užitečných odkazů na weby.
Programovací jazyk Python byl vydán v nové major verzi 3.14.0. Podrobný přehled novinek v aktualizované dokumentaci.
Bylo oznámeno, že Qualcomm kupuje Arduino. Současně byla představena nová deska Arduino UNO Q se dvěma čipy: MPU Qualcomm Dragonwing QRB2210, na kterém může běžet Linux, a MCU STM32U585 a vývojové prostředí Arduino App Lab.
Multiplatformní open source voxelový herní engine Luanti byl vydán ve verzi 5.14.0. Podrobný přehled novinek v changelogu. Původně se jedná o Minecraftem inspirovaný Minetest v říjnu loňského roku přejmenovaný na Luanti.
Byla vydána nová stabilní verze 6.10 (YouTube) multiplatformního frameworku a GUI toolkitu Qt. Podrobný přehled novinek v poznámkách k vydání.
Na regulární výrazy existuje několik pohledů. Pro ty, kteří je používat neumí, se jedná o magickou sekvenci znaků, které se nikdy nesnaží porozumět. Pro ty, kteří je používají, se jedná o mocný nástroj pro práci s textem, který lze použít při hledání, pro úpravy, nebo pro ověření vstupního řetězce. No a pro ty, kteří něco vědí o teoretické informatice, se jedná o větu jazyka typu 3. Navíc ta poslední skupina lidí tuší něco o konečném automatu a jeho vztahu k regulárním jazykům, výrazům.
Pochopitelně se nám tu vynořuje otázka. Pokud jsou regulární výrazy výsledkem gramatiky typu 3, to znamená nejméně mocné formy, proč se jimi vůbec zabývat? Proč nenasadit rovnou prostředky klasického programovacího jazyka, který je nepochybně mocnější a zvládne více věcí? Důvodů je několik. Předně síla jazyků typu 3 na většinu úloh stačí (a navíc současné výrazy u moderních nástrojů už patří do vyšších typů). Druhým důvodem je stručnost a (ne)přehlednost zápisu, oproti programové implementaci (jak se přesvědčíte dále). Kniha Art Of Unix Programming se v osmé kapitole zabývá minijazyky pro řešení specializovaných úloh, mezi něž se řadí i regulární výrazy. Obvykle je jednodušší napsat regulární výraz, než vytvořit jeho programovou implementaci.
Snad každého někdy napadlo — Jak to ten
Vezměme jednoduchý výraz grep (sed, perl, ...) vlastně dělá? Jaká je posloupnost kroků od zadaného výrazu až po kód, který jej provádí?x*y+, který značí vezmi libovolný počet znaků x, následovaný alespoň jedním znakem y.
Člověk, který o regulárních výrazech neslyšel, by pravděpodobně začal daný problém řešit asi takto:
AbcLinuxu.cz
ITBiz.cz
HDmag.cz
AbcPráce.cz
function hledej1(inp)
{
byloX = false; // promenne udavajici
byloY = false; // stav resene ulohy
zac = 0;
kon = 0;
for (i = 0; i != inp.length; i++) {
ch = inp.charAt(i);
if (!byloX && !byloY && ch != "x" && ch != "y") { continue; }
if (!byloX && !byloY && ch == "x") { byloX = true; zac = i; }
if (!byloX && !byloY && ch == "y") { byloY = true; zac = i; }
if ( byloX && !byloY && ch == "y") { byloY = true; }
if ( byloX && byloY && ch != "y") { break;}
kon++;
}
msg1 = "hledej1(\""+inp+"\") --> x*y+ ";
msg3 = "\n";
if (!byloY) { msg2 = "nenalezen"; }
else { msg2 = "nalezen (" + zac + ", " + kon + ")";}
return msg1+msg2+msg3;
}
Dlouho jsem přemýšlel, jaký jazyk zvolit pro příklady — C, C++, Javu, Python? Nakonec jsem se rozhodl pro Javascript a to z toho důvodu, že všechny příklady jsou jednoduché a navíc mohou být spuštěny přímo v prohlížeči. Bohužel mi dalo trochu práce ladění, protože se zdá, že některé konstrukce v jistých prohlížečích nepracují, jako třeba foreach (Opera, MSIE) a indexování řetězců (MSIE). Nicméně skripty jsou úspěšně otestovány v prohlížečích Mozilla Firefox 1.5, Internet Explorer 6.0 a Konqueror 3.5 a Opera 9.0. Výsledek (dynamicky generovaný Javascriptem) máte zde:
Je nutné poznamenat, že tento způsob implementace je velice (velice jemně řečeno) nevhodný. Kód je zmatený, složitý, špatně se chápe a tím poskytuje prostor pro chyby (ostatně moje implementace pracuje špatně). Navíc, byť i jednoduchá změna, znamená, že je nutné celý program změnit.
Tím, co kód znepřehledňuje nejvíc, jsou stavové proměnné. Respektive jejich složité vztahy, které musíme v programu uhlídat pomocí složitých podmínek. Pokud se nám v kódu (v lepším případě v návrhu) podobné věci množí, bývá konečný automat nejvhodnějším řešením. Formálně je (nedeterministický, bude vysvětleno dále) konečný automat pětice M = (Q, Σ, δ, q0 ∈ Q, F ⊂ Q)
Nejdůležitějším pojmem u konečného automatu je stav. Koneckonců se někdy nazývají stavovými automaty (Finite State Automata v angličtině). Automat lze graficky znázornit:
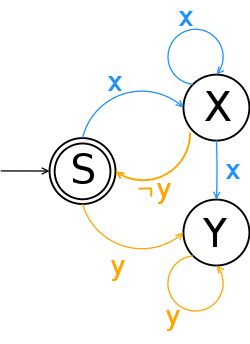
Jak vidíte, automat se sestává se 3 stavů S, X a Y, přičemž S je startovacím stavem a Y koncovým. Ne náhodou je tento automat ekvivalentní regulárnímu výrazy x*y+. Ve startovacím stavu S automat čeká na některý ze znaků x, nebo y. V případě příchodu znaku x se přepne do stavu X a ten neopustí, dokud nenačte znak y. Potom se přepne do stavu koncového stavu Y. Znak ¬y značí cokoliv mimo y, takže se ze stavu X můžeme dostat do počátku. Praktická implementace by mohla vypadat takto (přidal jsem 4. stav F, abych nemusel používat goto, nebo cyklus while):
function hledej2(inp)
{
states = {
S : 0,
X : 1,
Y : 2,
F : 3
}
st = states.S;
zac = kon = 0;
for (i = 0; i != inp.length; i++) {
ch = inp.charAt(i);
switch (st) { case states.S:
if (ch == "x") { st = states.X; zac = i;}
if (ch == "y") { st = states.Y; zac = i;}
break;
case states.X:
if (ch == "y") { st = states.Y; }
else if (ch != "x") { st = states.S; }
break;
case states.Y:
if (ch != "y") { kon = i - 1; st = states.F;}
break;
default:
break;
};
kon++;
if (st == states.F) { st = states.Y; break;}
}
msg1 = "hledej2(\""+inp+"\") --> x*y+ ";
msg3 = "\n";
if (st != states.Y) { msg2 = "nenalezen";}
else { msg2 = "nalezen (" + zac + ", " + kon + ")";}
return msg1+msg2+msg3;
}
Tato, byť na počet řádků delší, ale jednoznačně přehlednější implementace konečného automatu, je přesně to, co mnoho programátorů s úspěchem používá. Je nutné říct, že takto natvrdo
naprogramovaný stroj trpí špatnou rozšiřitelností, ale místo konstrukce switch case lze z výhodou použít hashovací pole.
Ovšem i toto řešení trpí malou obecností. Pokud chceme změnit regulární výraz, nezbude nám, než kód přeprogramovat (anebo použít dynamické jazyky a hashovací pole místo konstrukce case). Ovšem je tu ještě jedna možnost - jiný pohled na konečné automaty a to tabulka přechodů. Prakticky stejně jsou implementovány všechny pomocné knihovny pro konečné automaty.
| Stav | S | X | Y |
| x | X | X | S |
| y | Y | Y | Y |
| ... | |||
Ještě než budeme pokračovat, zbývá nám vysvětlit jeden pojem. Deterministický (DKA), versus nedeterministický automat (NKA). U DKA je přechod jednoznačně dán příští stav aktuálním stavem a podmínkou. NKA může mít na jednu podmínku následujících stavů více. Oba automaty jsou ekvivalentní, ale nedeterministické jsou rychlejší, protože nemusí prohledávat všechny možnosti a vyberou si vždy správnou větev. Nevýhodou je, že naše počítače, jak je známe dnes, jsou deterministické, což znamená, že nedeterministické stroje se stejně musejí převést na deterministické. Fragment NKA je zobrazen na následujícím obrázku.
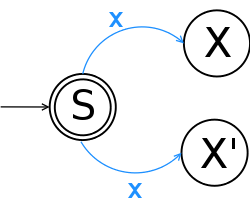
Mluvím o tom z toho důvodu, že běžně používaný algoritmus převádí regulární výrazy právě na NKA. Pokud se narazí na větev, která vede na více možností, program začne prozkoumávat jednotlivé cílové stavy (backtracking). Klasický postup skončí v případě nálezu prvního vyhovujícího výrazu. Posixová varianta v případě použité konstrukce "nebo" najde všechny vyhovující a vrátí nejdelší řetězec, ale tuto variantu běžné nástroje neimplementují, protože je nejpomalejší. Druhou možností je paralelní provádění všech cest, díky čemuž stačí jeden průchod a není třeba se vracet. Nevýhodou je skutečnost, že si nemůžete zapamatovat podvýrazy.
Toto byl pouze lehký úvod do problematiky konečných automatů. Zcela jsem vynechal problematiku stavových akcí, pojmy jako Mealy a Moorův automat. Nemluvili jsme o greedy regulárních výrazech a podobně. Navíc jsem tvorbu stroje pro provádění regulárních výrazů lehce odbyl. Jednak dnešní nástroje obecně regulární výrazy podporují. A v případě, že ne, je nejlepším způsobem jednoduše použít knihovnu PCRE (Perl Compatible Regular Expressions), která je syntakticky i sémanticky kompatibilní s regulárními výrazy Perlu. Což je defakto norma, protože skutečná norma POSIX se používá méně a její regulární výrazy nejsou tolik silné. Tuto knihovnu používají open source projekty Exim (pro nějž byla původně napsána), Apache, PHP, Postfix, nebo KDE.
Pokud chcete automaty vidět
na vlastní oči, podívejte se na Animace Teoretické informatiky, jedná se o flashové animace konečných (DKA i NKA) automatů, převodů NKA na DKA a mnoho dalších zajímavých věcí.
V dalším díle se zvolna přesuneme k problematice překladačů, na řadě je totiž syntaxe.
Nástroje: Tisk bez diskuse
Tiskni
Sdílej:
V případě příchodu znaku x se přepne do stavu X a ten neopustí, dokud nenačte znak yV tom případě máš drobnou chybku v obrázku u svislé šipky ze stavu X do Y.
deb http://ftp.cz.debian.org/debian jessie main contrib non-freedeb http://ftp.cz.debian.org/debian jessie main contrib non-freehledej1("y") --> x*y+ nalezen (0, 1)
To je velmi optimistický výsledek... 
Nemělo by to na osamocené „y“ mlčet?
No jo, dobrou a díky... 
Přečtu celé, až budu v použitelném stavu... 
2.8.2006 07:59
xvasek | skóre: 21
| blog:
| Zlín
Ještě by mě zajímalo, co je to "věta" (zmiňovaná v perexu a ještě v článku), já znám jenom písmeno (nebo symbol) a pak už jenom jazyk.
3.8.2006 08:39
xvasek | skóre: 21
| blog:
| Zlín
3.8.2006 13:16
Marek Bernát | skóre: 17
| blog: Arcadia
David
.
2.8.2006 22:50
lankvil | skóre: 8
| Praha
Moc pekny clanek, jak funguje grep me vzdycky zajimalo.
Jenom tenhle kus kodu mi prijde nejaky podezrely. javascript neznam, ale misto toho prvniho break bych videl radsi case ;)
2.8.2006 09:34
break states.Y:
if (ch != "y") { kon = i - 1; st = states.F;}
break;
. Jen drobnost: pokud me pamet nesali, tak u prvniho obrazku urcite neni koncovy stav Y, ale S, protoze v grafu se pocatecni stav oznacuje "sipkou odnikud do stavu" a koncovy (akceptujici) "dvojitym koleckem", takze na tom obrazku je S pocatecni a zaroven koncovy stav...
A pokud si chce nekdo trochu pohrat, doporucuju stahnout pekny simulator automatu v Jave ze stranek http://ozark.hendrix.edu/~burch/proj/autosim/
A navic je to proste bajecne nazorne. Je to parada.
Jen bych se mozna primluvil za to, aby uvadene priklady byly spravne. Sice jsem si s prvni implementaci x*y+ hral, ale zrovna mne nenapadla kombinace, na ktere je chyba tehle implementace videt a z toho kodu jsem to taky nejakou dobu musel lustit nez jsem prisel na to co je blbe a jak to (mozna, nemam overeno) udelat spravne. Popravde, kdyby to autor nezminil, tak bych na chybu sam od sebe asi neprisel.
Jinak mam teda par laickych dotazu:
Ad sipka X, Nechapu proc je v prvnim obrazku (SXY) u prechodu X->Y sipka oznacena X, a to ani po upozorneni Kralik_, ze je to NKA (coz si nejsem moc jisty). Podle "selske" logiky bych tam dal Y. Jsem ve stavu X, kdyz narazim na dalsi X, tak zustavan ve stavu X (kruhova sipka k X oznacena X), kdyz narazim na cokoliv jineho krome X a Y tak jdu zpet do S (sipka k S oznacena !y, coz je skoro jako S ) a pokud narazim na Y tak jdu ze stavu X do stavu Y (sipka oznacena X?!, to mi spis sedi Y, jak navrhoval diverman v druhem prispevku).
Dotaz 1: proc je tam X ?
Ad NKA, na mne to schema spis pusobi pomerne "urcite" co se tyce pravidel pro prechody mezi stavy. Pokud neco, tak bez touto a jenom touto cestou tamhle.
Dotaz 2: proc by to mel byt NKA ?
Ad konecny stav, pochopil jsem notaci, ze sipka od nikud do stavu oznacuje start a dvojite kolecko oznacuje konecny stav. Coz zjevne vypada jak bylo zmineno vyse, ze zacatek je shodny s koncem. Dava to v teto uloze smysl ?
Dotaz 3: kde je teda konecny stav ? A pokud je v S tak proc ?
Ad prechodova tabulka, jasne a pochopitelne az na nezodpoveznou poznamku divermana o prechodu Y->S po precteni x
Dotaz 4: jdu skutecne do ... S po precteni x ve stavu Y ? Pokud ano, melo by to byt v obrazku ?
Ad ostatně moje implementace pracuje špatněPomohla by pridat pred posledni podminku jeste jednu ?
if ( byloX && !byloY && ch != "y") { byloX = false; zac = 0; kon = 0;}
Dotaz 5: Opravil by muj navrh na pridani podminky tu implementaci ?
Diky moc za pripadne odpovedi a srry za takovou zbesilou tapetu, ale pro lidi co nemaji potrebnou vysokou skolu je dobre, kdyz se i v trivialitach ujisti. Je to lepsi nez stavet na necem co je blbe
) "akceptujici stav". Tento stav neni vyjimecny tim, ze se v nem vypocet zastavi, jak by mohlo napovidat slovo "koncovy", ale tim, ze pokud dojdou pismenka na vstupni pasce a automat je zrovna v tomto stavu, pak je slovo "akceptovano", tedy uznano za spravne. Pokud by dosla pismenka a automat byl v jinem stavu, nez v nekterem z akceptujicich, je slovo zamitnuto, tedy prohlaseno za spatne. Pekne je to videt pri simulaci v tom simulatoru, co jsem dal odkaz vyse.
Ad 4: Ve stavu Y smim cist jen znaky y. Spravne by mel mit automat jeste jeden neakceptujici stav (jednoduche kolecko), kam by byl automat "nasmerovan", pokud by ve stavu Y precetl cokoliv jineho nez y. Sipka not(y) do S je taky zbytecna, protoze predpokladam, ze mame abecedu {x,y}, takze not(y) je x a pod tim se cykli nad X (prechod do S vnasi jen nedeterminicnost a vynucuje dve x za sebou). Pokud mel autor na mysli "sirsi" abecedu, pak ma not(y) jit do zmineneho noveho neakceptujiciho stavu, protoze slova obsahujici jakykoliv jiny znak nez x a y neodpovidaji x*y+. Navic prechod do S umoznuje akceptaci slov jako treba xzxy, coz jiste neodpovida x*y+, tedy pokud se bavime o automatech a ne o vyhledavani retezce x*y+ v nejakem jinem retezci. To take implikuje, ze z Y pod x rozhodne nejdeme do S. Umoznili bychom akceptaci napr. slova xyxy a to neodpovida x*y+, ackoliv tento "patern" obsahuje hned dvakrat. Samozrejme je tu opet ona nejasnost, jestli se bavime o automatech nebo o implementaci vyhledavani regularnich vyrazu v retezci za pouziti automatu. Ze clanku mi to neni zcela jasne.
Y je koncovy stav proto, ze pokud jsme v nem, mohli jsme projit lib. poctem pismen x a alespon jednim y (at uz to y bylo bez x nebo ne).
A jestli by ten navrh opravy neco spravil se mi opravdu ted nechce zjistovat. Ten kod je totalne necitelny, jak pravil koneckoncu i autor
To x nad sipkou ze stavu X do Y je samozrejme spatne -- patri tam y (to je to alespon jedno y, ktere tam musi byt kvuli +). NFA je to proto, ze z jednoho stavu vede vice sipek s x. To je ten nedeterminismus. Konecny automat cte ze vstupni pasky jednotliva pismenka a kdyz dorazi do stavu X a zrovna ma cist dalsi pismenko x, tak nevi, kudy ma jit. Pokud by byl ten obrazek spravne (viz vyse), bude ten automat DFA (deterministicky), protoze v zadnem ze stavu neni moznost jit vice jak jednou cestou skrze jeden znak.Njn, pokud je nad sipkou "y" a pokud not(y) znamena cokoliv jineho krome x a y, pak nepovede z jednoho kolecka vice sipek ze stejnym pismenkem => je to spis DKA podle toho co rikas. Pokud ale not(y) zahrnuje i moznost "x" (bezohledu na to, ze tato moznost uz je tam konkretne zminena tou kruhovou sipkou), pak opravdu bude kolecko X s vice stejnymi moznostmi "uniku" a pak je to jednoznacne NKA jak pises. A pokud by byl obrazek spravne tak by opet bylo vice stejnych vetvi s jednoho kolecka a pak by to spis byl NFA ne ? Ted mi teda zbyva otazka, jak je to s tim not(y) v tomto pripade ? PS: jinak ostatni bylo velice pochopitelne napsano, diky :-}
. Nuze k tomu "not": nejak si nevybavuju, ze bychom ho vubec v automatech pouzivali. Kazdopadne bych to not intuitivne definoval tak, jak to byva obvykle, tedy not(y) je vsechno krome y (nezavisle na jinych sipkach do jinych stavu). Spis si vybavuji, ze jsme nad sipku vypisovali vsechny znaky, pod kterymi se do daneho stavu prechazi. Je to proto, ze se automaty vetsinou probiraji nad nejakou "malou" abecedou, napr. {x, y} nebo {a, b, c, d}, aby to bylo nazorne a prehledne. U toho obrazku postradam exaktni definici abecedy, nicmene pokud jsme si ve cvikach abecedu nedefinovali, vzdycky jsme pocitali s tim, ze abeceda ma jen pismenka obsazena v grafu. Proto je to "not" ponekud nelogicke. Pri abecede {x,y} je not(y)=x. Pokud ma mit abeceda vice pismen, pak chybi definice (a navic jsou pro tuto ulohu jina pismena zbytecna).
A ted k te determinite:
Tak jak je to v obrazku je to jednoznacne NEDETERMINISTICKE (NFA) a to kvuli stavu "X". Z nej vede smycka pod x, sipka do Y pod x a sipka do S pod not(y), coz je take x.
Pokud obrazek opravime, odstranime not(y), ktere je chybne, a zamenime x za y v preklepu pri prechodu z X do Y, pak je to DFA, protoze z S jde po jedne sipce pod x a pod y, z X jde smycka pod x a sipka pod y a z Y je jen smycka y. Nikde tedy neni vic jak jedna sipka z jednoho stavu pod stejnym znakem. (Samozrejme tou opravou myslim opravu chyb v obrazku a ne algoritmicky postup, jak prevest NFA na DFA.)