Jak se píše procesor

8. 7. 2005 | Luděk Crha | Programování | 19337×

Počítač má dnes skoro každý. Většina lidí také ví, že jeho základním prvkem je procesor. Víte ale, jak se takový procesor dá vytvořit? Zamysleli jste se někdy nad tím, čím je dána maximální frekvence procesoru? Je možné si navrhnout a vyzkoušet vlastní procesor "doma"? Na tyto a podobné otázky odpoví tento článek.

Úvod

Nejdříve uvedeme základní pojmy. Z pohledu návrhu je procesor číslicový obvod. V číslicovém obvodu je třeba definovat dvě základní úrovně signálu - logická '0' a logická '1'. Číslicový obvod se skládá z hradel a propojení mezi nimi. Hradlo je elementární prvek, který realizuje základní funkci. Zde je příklad realizace logické funkce AND.

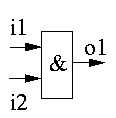
Hradlo na obrázku má dva vstupy a jeden výstup. Pokud je na obou vstupech '1', na výstupu hradla bude '1'. Při jakékoliv jiné kombinaci vstupů bude na výstupu '0'.

My budeme používat hradla realizující logické funkce AND, OR, NOT a XOR. S těmito hradly již můžeme vytvořit libovolnou logickou funkci. Něco nám ale pořád chybí - a to je paměťový prvek, který by pomohl vnést do našeho obvodu časovou závislost. Použijeme hradlo typu D, které si dokáže pamatovat hodnotu.

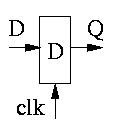
V okamžiku náběžné hrany (přechod z '0' do '1') hodinového signálu clk se na výstup Q zapíše hodnota vstupního signálu D, jinak zůstává hodnota na výstupu nezměněna. Na následujícím obrázku je znázorněn příklad časového průběhu, který demonstruje toto chování.

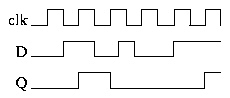
Hradlo D tedy funguje velmi jednoduše, ale, jak si ukážeme dále, spolu s pomocí logických hradel nám umožní navrhnout celý procesor.

Návrh obvodu

Teď, když máme základní stavební prvky, můžeme začít navrhovat obvod. Ale jak? Existují návrhové systémy, kde graficky skládáme obvod z hradel a ta propojujeme. Pro složitější obvody je však tento přístup takřka vyloučen. Naštěstí existují jazyky, které nám umožní textově popsat strukturu obvodu. Jejich syntaxe je velmi podobná programovacím jazykům. V této podobnosti je ale skryto jedno velké nebezpečí - nemusíte si ani uvědomit, že popisujete hardware a nepíšete program. My budeme používat jazyk VHDL (VHSIC Hardware Description Language), který je u nás nejrozšířenějším jazykem pro návrh.

VHDL

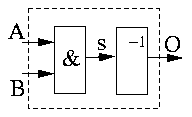
Základní prvky ve VHDL jsou entita a architektura. V deklaraci entity definujeme vstupy a výstupy obvodu, pomocí architektury tvoříme vlastní obvod. Dalším důležitým pojmem je signál, základní propojovací prvek. Signál si můžeme představit jako vodič, kterým spojujeme hradla. Vstupy a výstupy definované v entitě jsou také signály. Základem pro vytváření obvodu je příkaz přiřazení <=, který signálu na levé straně přiřadí hodnotu na pravé straně. Všechny uvedené pojmy si ukážeme na jednoduchém příkladu, realizaci obvodu na následujícím obrázku:

-- dve minuska jsou komentar
ENTITY jednoduchy_obvod IS -- entitu nazveme jednoduchy_obvod
PORT (                     -- klicove slovo PORT
   A, B: IN std_logic,     -- dva vstupy, A a B (typ std_logic
                           --   znamena bezny vodic)
   O: out std_logic        -- jeden vystup
);
END jednoduchy_obvod;      -- konec deklarace entity

ARCHITECTURE moje_architektura OF jednoduchy_obvod IS
                           -- tvorime obsah entity
signal s: std_logic;       -- vytvorim si pomocny signal
BEGIN                      -- zacatek tela architektury
   s <= A and B;           -- v signalu s bude logicky soucin
                           --   signalu A a B
   O <= not s;             -- na vystupu O bude negace s;
END moje_architektura      -- konec architektury

V deklaraci entity definujeme vstupy obvodu A a B a výstup O. Tím říkáme, jak bude vypadat obvod z vnějšku. Architekturu (tedy vnitřek obvodu) přiřadíme k entitě a v deklarační části si vytvoříme pomocné signály, v našem případě jediný signál s. V těle architektury (za klíčovým slovem begin) již píšeme schéma obvodu. V signálu s chceme mít logický součin signálů A a B. To implikuje vytvoření hradla AND. Na výstup O přiřazujeme negaci signálu s, což vede na vytvoření hradla NOT mezi signál s a výstup O.

Pokračování

Příště si ukážeme, jak vytvořit složitější obvody, a jakým programem si můžete VHDL kód odsimulovat na vašem PC.

       

Komentáře

[Palo]

Jedna mala nepresnost (ak som uplne vedla tak ma opravte :o) ) je, ze hradlo je riadeny spinac t.j. na zaklade vstupu prepaja informaciu na vystup (v priapde obojsmernych hradiel sa to neda takto jednoznacne povedat). Este existuju aj viacstavove hradla (zvacsa pri zberniciach, ktore maju aj nejake kontrolne signaly t.j. urcuju priepustnost/nepriepustnost hradla).

To co realizuje logicke operacie su logicke cleny (podla def. je logicky clen elementarny cislicovy system ktory realizuje operacie nad boolovskou mnozinou). Cize abstraktne povedane sa logicke operacie vykonavaju cez logicke cleny, ktore mozu byt realizovane cez nejake konkretne typy hradiel. Ale myslim, ze to nie je podstatne..

Clanok je velmi dobry, uz sa tesim na pokracovanie

[David Jež]

Ono je to tak, že zatímco hradlo je spíše ,,technologický`` pojem, tak logické členy jsou pojem vyšší úroveň abstrakce. A protože logické členy jsou ve finále zrealizovány pomocí hradel, tak se (jako všude jinde) nakonec stejně ve vyšších vrstvách abstrakce mluví o členech jako o hradlech. Pokud se bavíš o funkcích, bereš logické členy jako elementy na kterých stavíš a souhrně je nazýváš hradly, protože jimi jsou stejně tvořeny a spoléháš na to, že je to jedno a každý ví o co jde. A pokud se pohybuješ níže, tak tě zase zajímají jednotlivé realizace, přechody, cesty a další legrace, takže ti to je také jedno. Nicméně pokud se na to díváš s analogového pohledu (tedy klasická elektronika) tak to jedno není, protože jsou to pro tebe opravdu jiné součástky. No je to trochu zmatené, ale však určitě chápeš, hej?
-djz

[David Jež]

To snad není možné, asi únava: s/s analogového/z analogového a dál to raději nečtu...
-djz

[profesor]

Článek je super, první odstavec se učí na střední škole rok, druhý odstavec na vysoké škole celý semestr. Že já jsem to absolvoval, ztráta času. Místo toho jsem mohl počkat na seriál na abclinuxu a sfouknout to v pětiminutovém kursu. Už se těším na další díly. Ve druhém to tak nějak dokončíme, ve třetím navrhneme podpůrné obvody a ve čtvrtém na to konečně nainstalujeme Linux (čímž se potvrdí že sem tento super seriál tematicky patří).

[David Ondřich]

Člověče, že ztrácíš čas psaním komentářů... Kdybys chvíli gůglil, za dobu, cos psal ten příspěvek, jsi mohl mít "vystudovanou" nejmíň ekonomku. :-P

[ero]

lol :D ..dobry komentar :)

[JA]

Co vam vadi na tom clanku? mam z vas pocit, ze ak nahodou dakto zvas sa naucil jednu poucku (co je to hradlo) tak uz je najmudrejsi na svete a hned zautoci na autora clanku, aby mu ukazal, ze je sprosty. Bezna vlastnost Cechov a Slovakov. Opovrhovat inymi, typicka pre deti v skolke ktore sa hadaju, kto je lepsi. Som z vas sklamany.

[DjAARA]

Ja si nevsiml, ze by nekdo hanil autora. Ale mam ted jenom jedny oci, takze mozna vidim spatne. Az si nasadim bryle (nemuzu je najit :D), tak to proctu jeste jednou... Ale stejne bude vysledek stejny.

Jsem z tebe zklamany :o).

[Palo]

Ospravedlnujem sa ak moj prispevok vyznel, ze som chcel zautocit na autora, alebo nejako uberat z hodnoty clanku. Ako som napisal, clanok je perfektny. Myslim ze diskusia pod clankami sluzi na vyjasnenie nepresnosti ktore su v clanku (co nie je tento pripad!) alebo jeho rozsirenie o dodatocne informacie (linky, terminy, odkazy...). Prispevok som uviedol aby som upresnil terminy (ktore som napisal ze pre clanok nie su podstatne), keby sa niekto s takym dacim stretol a nevedel co to je. Ak terminy ktore som uviedol zneju prilis nabiflene a definitoricky, tak to nie je moja chyba, myslim, ze presne vyjadrovanie je sucastou prirodnych vied a takuto definiciu najdete v prvych riadokoch skoro kazdych skript popisujucich dane cleny v architekture pocitacov.

[David Jež]

Ne, v pořádku. Tvé připomínky jsou konstruktivní a k věci a je vidět, že víš co chceš říct. Spíše zde šlo o kritiku ,,profesora`` a jeho ironii o vystudování za 5 minut. Což tak sice působit může, ale chtěl bych ho vidět, jaký by sám udělal jiný úvod. Aby pro lidi, kteří vůbec neví, která bije, působil jako nakopávač co je třeba vědět a o čem se jedná dále a pro ostatní působil jako úvod. A problematika je natolik rozsáhlá, že jsem si do nedávna myslel, že udělat do ní krátký úvod vypichující vše podstatné nelze nebo jen velice obtížně. Do nedávna proto, že na přednáškách v nějakém šíleném předmětu pro informatiky, vysoká teorie o objektech, která s tím vůbec nesouvisí, mě Karel Masařík i Luděk přesvědčili že to možné je, udělat jednu takovou přednášku, kterou by ti teoretici co to v životě neviděli pochopili a ostatním nepřišla nudná. Ale já bych to dělat něchtěl, protože by mi jedna dvoj- nebo troj- hodinovka nestačila a neměl bych na to právě kvůli podobným ,,profesorům`` nervy...
-djz

[megi]

Jsem zvědavý, jestli dojde i na ghdl. :)

[David Jež]

Jak znám Luďka (zdravím Tě, koukám že si nedáš pokoj ani o prázdnínách, což je fajn, díky za článek a nezapomeň tam napsat také něco pro nás ! Jinak co že ses rozhodl psát na linuxový portál? Už se těším na pokračování, dojde i na ADL, ISDL a tato témata? A určitě také plz. popiš tu novou latch-like šílenost od Intelu, jsem líný si ji hledat.) tak určitě spíše na Model Sim. Jinak já osobně používám knihovny z FreeHDL, na testy vanilla CAD, sice z tabulek (zvlášť u složitého návrhu) by Luděk lezl po zdi , ale je tam dobře vidět distribuce signálu a rozepsané i to, co se děje ,,okamžitě`` což se někdy hodí. Docela mi vyhovuje Sonata. Ještě bych rád rozjel Alliance, zvláště ten její syntezátor a router mě zajímá, ale k tomu jsem se zatím ještě přes zaneprázdnosti v jiných oblastech nedostal. To mi tak připomíná, že bych mohl někdy do blogu zapsat sumarizaci letošního semestr a rozepsat návrh našeho miniprocesůrku (spíše chytřejšího XORu...), což za zablogování celkem stojí .
-djz

[Luděk Crha]

Ahoj, diky za reakce v diskusi. Pro Tebe tam toho asi moc nenapisu , clanek chci koncipovat jako uvod do VHDL, zaverem by mohl byt navrh casti nebo celeho procesoru ve VHDL. Hlavni duraz chci klast na klasicke rozdeleni registry-logika, takze "latch-like" procesor pri te prilezitosti zminim. Taky diky vsem za zivou diskusi, i na jejim zaklade se muze vyvijet obsah dalsich dilu. Za chvili mizim na tyden na dovolenou, tak pekne prazdniny!

[Jakub Hegenbart]

Proč se patlat s registry? Proč ne třeba něco z ML0 kategorie?

[Michal Pokorný]

Článek je super, těším se na další díl. Jsem rád, že se tu konečně někdo začal věnovat využití Linuxu v oblasti návrhu elektronických systémů.

[Jan Prech]

Nahodou, takhle zhusteny uvod do VHDL, ktery i pri te zhustenosti vicemene nelze, klobouk dolu...
Ostatne, dokud se nezacne syntetizovat, tak je VHDL celkem sranda...

[petr_p]

Jen tak pro poradek na uplny log. system staci napr. jen (AND, NOT).

[David Jež]

Jen tak pro pořádek, buďto dvojice jeden z (AND, OR) a NOT, což se používa spíše jen na papíře a uvádí se souhrně trojice AND, OR, NOT, což by ale v praxi s reálnými součástkami nikdo nedělal. Nebo jeden NAND. Nebo jeden NOR. Nebo jeden XOR. V praxi se používá NAND nebo NOR, protože je nejmenší a případně pokud to zjednoduší tak invertor, protože je menší než jeden NAND. Ta kombinace reálných součástek AND a invertoru je blbost největší proto, že místo jednoho např. šesti tranzistorového NANDu použít osmi tranzistorový AND a k tomu dvou tranzistorový invertor může napadnout jen vola .
-djz

[Michal Kubeček]

Pokud si dobře vzpomínám, v 7400 byly jen čtyři traznistory na jedno hradlo…

[Jakub Hegenbart]

Jeden o voze, druhý o koze...

Ach, pardon: Jeden o CMOS, druhý o TTL...

[Jirka]

Jste si jisty, ze to jde i XORem? Myslim ze to jde jen pomoci NAND nebo NOR, dokonce se to jmenuje podle dvou chlapiku (uz si nevzpomenu). Jestli i XOR, rad se necham poucit.

[llook]

Myslím, že se to jmenuje de Morganův vzorec:

~(a | b) == ~a & ~b;

A naopak:

~(a & b) == ~a | ~b;

A taky myslím, že s xorem to nijak nejde, ale nevím - o takové věci se moc nezajímám.

[raziel]

pana Beka tak ten sa ma tymto natrapil. Inak clanok sa bol dobry :)

[Jirka]

Tak jsem si to nasel. Je to Shefferova algebra (NAND) a Piercova algebra (NOR).

[Martin Tůma]

XOR netvoří úplný systém logických spojek (samotým XORem nelze realizovat např. negaci). Nicméně množina {XOR, T} (T je tautologie) již úplný systém logických spojek tvoří. T pak v praxi není nic jiného než logická "1", takže pomocí XORu lze zkonstruovat libovolný logický obvod.

[David Jež]

Přesně tak, potřebuje to log 1, protože xor samotný dokáže udělat akorát negativní tautologii (a XOR a = 0). Potom už se dá realizovat i invertor (XOR s log 1) a další. Akorát jste mě teď všichni zaskočili s tím, jestli s ním lze realizovat opravdu jakékoliv libovolné funkce. To by se muselo dokázat na papíře, ale žil jsem od střední v domnění, že to je už někým jako algebra popsané (pierce je opravdu XOR nebo NOR?). Ale jestli ne libovolnou funkci tak alespoň velkou množinu funkcí, protože vím, že jsem v automatizaci zjednodušoval XORem hodně a prakticky pořád a zabíralo to málo součástek. Ovšem jestli by to bylo úspornější i technologicky (myslím si že ne) už je věc jiná .
-djz

[Martin Tůma]

Jaj už jsem psal, množina {XOR, T} tvoří úplný systém logických spojek, takže pomocí těchto dvou operátorů opravdu lze složit libovolnou funkci. Úplných systémů logických spojek je celá řada, výjmečnost Shefferovy algebry (NAND) a Piercovy algebry (NOR) je pouze v tom, že zde je úplný systém logických spojek tvořen jednou jedinou spojkou.

P.S: "negativní tautologie" se většinou nazývá kontradikce

[Michal Kubeček]

Jaj už jsem psal, množina {XOR, T} tvoří úplný systém logických spojek, takže pomocí těchto dvou operátorů opravdu lze složit libovolnou funkci.

Tak jsem si to znovu rozmýšlel a obávám se, že nemáte pravdu. Položme

  Af = f(0,0) ^ f(0,1) ^ f(1,0) ^ f(1,1)

Pak elementárně A(f^g) = (Af) ^ (Ag) (XOR je komutativní a asociativní), ale problém je v tom, že pro všechny vaše stavební kameny (x,y,1) je Af rovno nule, takže vzhledem k výše uvedenému z nich nikdy nemáte šanci poskládat cokoli s Af = 1, např. AND. (Lidově řečeno: řekneme, že funkce je sudá, jestliže má v tabulce sudý počet jedniček. Snadno nahlédneme, že XOR dvou sudých funkcí je opět sudá funkce a protože funkce vracející první argument, funkce vracející druhý argument i tautologie jsou sudé funkce, nikdy z nich nesložíte lichou.)

[Martin Tůma]

Máte samozřejmě pravdu, úplný systém logických spojek tvoří až množina {XOR, T, AND či OR} (nebo jiná "větší" množina s XORem). Jdu si na studijní nechat zrušit zkoušku z matematické logiky...

[Pavel Tišnovský]

Zjednodušeně řečeno to lze dokázat ve dvou krocích:

1. Nejprve musíte dokázat, že jakákoli logická funkce více proměnných lze napsat pomocí funkcí dvou proměnných a negace (funkce jedné proměnné). To samozřejmě dokázat lze, pro booleovské operace platí "běžná" pravidla, jako je asociativita, komutativita atd.

2. potom stačí pro vybranou funkci zjistit, zda pomocí ní lze realizovat všech šestnáct binárních funkcí dvou proměnných (s využitím výše zmíněných pravidel a de Morganova pravidla). To stačí pouze rozepsat na papíře a hned máte výsledek.

[asym]

Jedine NAND, jsem odchovany logitronikem :)))

[peto]

Dufam, ze bude nieco aj o FPGA, alebo aspon o GAL, vobec nic o tom neviem zohnat a len koli tomu nepojdem na techniku...
Napr. co sa da od tychto obvodov ocakavat, ake su rychle a hlavne ako sa pouzivaju.

[Jakub Chalupnik]

Muzes se mrknout treba na Wikipedii: http://en.wikipedia.org/wiki/FPGA

Velice strucne a obecne receno - FPGA/GAL jsou obvody, ktery obsahujou jakysi univerzalni logicky cleny a ty si je muzes libovolne popropojovat a vytvorit tak libovolnou funkci. Propojovani se dela tak, ze se do dany soucastky "nahraje" program, kterej ji rika, co a jak propojit.

GAL je zastupce takzvanych PLD (Programmable Logic Device) - je velice jednoduchej, obsahuje jen nekolik desitek az stovek logickych clenu. Vyrabi je spousta firem a jsou vicemene stejny. Dalsim stupnem jsou CPLD (Complex PLD), ktery jsou o neco slozitejsi. FPGA (Field Programmable Gate Array) obsahuji tisice az miliony logickych clenu, casto i pamet RAM a dalsi.

[David Jež]

Zajdi si do knihovny a pujč si skripta z VUT FEKT Ing. Kolucha o programovatelných obvodech. Tam se dozvíš základ. Konkrétní realizace viz. datascheety a pokud chceš něco obecně o programování jednotlivých zástupců, protože zde je to tak trochu každý pes jiná ves, tak hledej na googlu nebo někde v archivu fórka na willem.org byl odkaz na celkem dobrý textík vysvětlující alespoň nejběžnejší způsoby.
-djz

[Luděk Crha]

O techto vecech se chci ted zminit jen uplne okrajove, nechci delat serial moc slozity. Ale na konci, v pripade zajmu, muzu pridat jednu kapitolku jen o synteze a hradlovych polich.

[pavel prochazka.zde.cz]

Dobry den, ma mejch www strankach je taky neco malo o VHDL a CLPD, a neco o PICech... tak pokud mate nekdo zajem muzete tam hodit ocko...